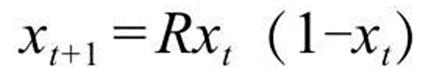零、前言
这是一篇关于复杂系统在游戏设计中应用的文章,整篇文章分为三大部分,第一部分介绍复杂系统和涌现,第二部分借由复杂系统提出一种新的度量游戏的方法,第三部分会通过实际的原型设计,来深入探讨复杂系统和涌现在设计中的应用方式。
温馨提示,全文字数3w+,预计阅读时间较长,欢迎关注收藏慢慢看,一家之言,抛砖引玉,也欢迎各位朋友交流斧正。
一、复杂系统简介
首先,复杂系统是什么?
复杂系统有很多定义,比较简洁的定义是:由大量相对简单的自组织个体构成,个体之间通过简单的规则交互,却能涌现出复杂宏观行为和现象的系统。
蚁群,大脑,经济系统,免疫系统,生态系统,互联网,元胞自动机,人类社会等等,都是复杂系统。
这里的复杂系统定义有两个关键词,自组织(self-organizing)和涌现(emergent)。
“自组织”是指系统内部或外部没有一个指挥者,告诉个体该怎么做,而是个体自身通过规则控制自身。
“涌现”,就是指系统组成部分间简单的互相交互,却在宏观层面产生了新的特性或行为,这些新特征或行为称为“涌现”。这是非线性系统的特征,即1+1>2,另一种说法就是整体大于部分之和。
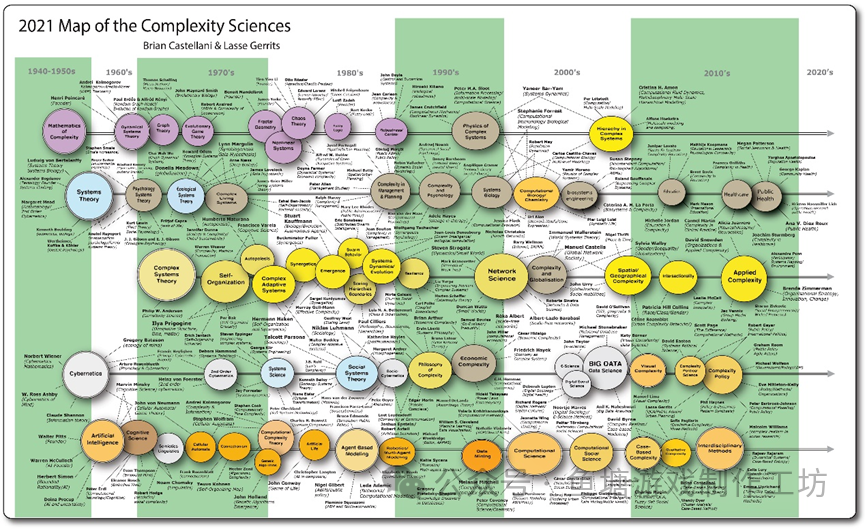
复杂系统研究是一个跨学科的科学研究,涵盖了许许多多分支,下图是复杂系统科学的分布图,来源网站https://www.art-sciencefactory.com/complexity-map_feb09.html:
对复杂系统研究的重视比较晚,目前也处于探索之中,没有公认的定义,统一理论或一般性原理。对不同复杂系统的共性探索一直是重中之重,不同领域的科学家提出了自己的理论,但还未完全达成共识。
而我们只关注复杂系统在游戏中的应用,一般来说,复杂系统在游戏中的应用分两个大方向:
- 以代理(人,动物,AI等)为核心的复杂系统,例如蚁群,公司,社会,经济系统等。沙盒,故事生成器类游戏用的比较多,例如kenshi,《模拟人生》系列,环世界,矮人要塞等等。
- 以客观规则为核心的复杂系统,例如基于物理化学规律的湍流,天气,N体运动等。物理模拟类游戏,应用主动布偶的游戏,编程类游戏,某些建造组装类游戏等等
当然两者也可以结合,但一般因性能和复杂度考量,都会有所侧重。
笔者最近的两个游戏也深入应用了复杂系统和涌现的设计元素,最近的游戏《流浪方舟》利用了物理系统作为复杂系统,为我们产生有利的碰撞位移涌现,是以客观规则为核心的复杂系统利用。
而上个游戏《追随者联萌》中实现了GOAP和行为树结合的AI,令整个NPC的行为交互组成一个复杂系统,是以代理为核心的复杂系统。关于GOAP的介绍,可以参考笔者之前的一篇介绍文章:
https://mp.weixin.qq.com/s/U9CmZ2uTEv91KPosHDFZRQ
总而言之,复杂系统为我在游戏开发领域,不论是技术还是设计,提供了很多不同的思考角度,是一个非常有用的工具。因此,本篇文章就是结合我的一些实践和思考,跟大家简单分享交流一下。
接下来三章,我们通过复杂系统中非常具有代表性的混沌系统,来揭开复杂系统的面纱一角。
二、混沌的发端,动力学与预测
人们讨厌宿命论,却总想着预测未来。
——我说的
首先我们简单介绍一下动力学。
动力学始于亚里士多德朴素但错误的运动理论,后来伽利略,哥白尼,开普勒以实验观察推翻亚里士多德流行了1500年的理论,再到牛顿横空出世,发明了微积分,正式创建了经典力学。提出了著名的牛顿三定律:
- 在任何情况下,一切物体在不受外力作用时,总保持静止或匀速直线运动状态。
- 物体的加速度与物体的质量成反比。
- 两个物体之间的作用力和反作用力,在同一条直线上,大小相等,方向相反。
在牛顿进一步提出万有引力定律后,在当时,牛顿力学完美地解释了一切物体的运动,其适用于任何大小的物体,不论是落下的苹果,还是燃烧的太阳。理论上,人们若是知道一个物体的初始位置和速度,就可以计算出后续的运动,自然就有聪明的小朋友想到:若是知道宇宙中某一刻所有粒子的当前状态,那是否就可以预知后面任何时刻的宇宙状态。
上述精确预测的假说就是著名的“拉普拉斯妖”,数学家拉普拉斯在1814年说:
“我们可以把宇宙现在的状态视为其过去的果以及未来的因。如果一个智者能知道某一刻所有自然运动的力和所有自然构成的物件的位置,假如他也能够对这些数据进行分析,那宇宙里最大的物体到最小的粒子的运动都会包含在一条简单公式中。对于这智者来说没有事物会是含糊的,而未来只会像过去般出现在他面前。”
如今,我们有强大的计算机,无需一个多智近妖的智者,也许未来有了足够强大的计算机就能做这个工作。如果真是如此,岂不是宇宙中的一切都已经注定,像一个上完发条的钟表,遵循三定律一直循规蹈矩地走下去,这是一个多么绝望的“决定论宇宙”啊。
还好1927年,海森堡(Werner Heisenberg)提出了量子力学中的“测不准原理”,证明不可能在准确测量粒子位置的同时,又准确测量其动量。如此,在微观世界的准确预测梦破碎,也慰藉了不愿相信宿命的人。
统计力学与预测
海森堡测不准原理只针对微观情况,而玻尔兹曼(Ludwig Boltzmann)创建的统计力学告诉我们,即使无法计算微观尺度的每个分子的运动,也可以用统计学的方式预测大量分子整体上的平均位置和速度,当粒子数量足够多时,他的方法“几乎总是对的”。统计力学是链接热力学和经典力学的桥梁,气压,热力学第二定律都能很好的用统计力学来解释。那么即使微观尺度上无法预测,宏观尺度上,是否可以通过统计学方式来预测系统的整体变化呢?
答案是不行,下面就是大名鼎鼎的混沌系统出场的时候了。
三、混沌系统
有时初始条件的微小差异,将造成最终现象的极大改变。前者的小误差,会造成后者极大的错误。预测将成为不可能的事,我们面对的是偶发现象
——庞加莱,《科学与方法》,1908年
1959年,42岁的数学和气象学家爱德华·罗伦兹(Edward Lorenz,1917—2008)在尝试用一个原始的计算机来预测天气,结果发现输入参数时微小的差异会造成两次结果完全不一样,即使两次预测计算机每一步的计算方法都一样。
后来,罗伦兹在一场学术会议上发表了论文来探讨这种对初始条件十分敏感的天气系统,论文题目叫——《巴西的一只蝴蝶舞动翅膀,可以引发得州的龙卷风吗?(Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas?)》,这就是著名的“蝴蝶效应”(The Butterfly Effect)。
天气系统就是一个典型的混沌系统,这里可能有点反直觉,为什么有些系统对初始条件就这么敏感?答案在于混沌的“非线性”和“自我引用”特性。
下面介绍一个经典的可以体现混沌本质的数学抽象——逻辑斯蒂映射(logistic map),它非常简单,其特性又非常令人震撼和着迷,我第一次读到时有种醍醐灌顶的感觉哈哈。这里主要引用梅拉妮·米歇尔的著作《复杂》的逻辑斯蒂映射一章,非常推荐大家读读这本复杂系统的科普读物。
这是逻辑斯蒂映射的方程:
X(t)是当前值,X(t+1)是下一步的值。R是一个参数,我们可以自己调,先不管。我们要做的很简单,定一个R,然后以一个介于0-1之间的X(0)开始,代入这个公式,得到X(1),然后把X(1)代入公式,以此类推不停得到新的值即可。这就是一个非常简单的“非线性”的方程。
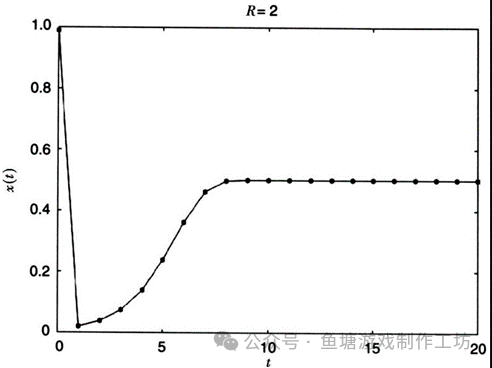
让我们试试R=2时会怎么样,我们会发现有意思的事情,就是不管X(0)输入的是什么值,最终X(t)都会停留在0.5这个值,这个0.5正是所谓的不动点(fixed point):到达这一点所花的时间依赖于出发点,但是一旦到达就会保持不动。当R=2.5时,你同样会发现系统到达一个不动点,不过这次不动点是0.6。
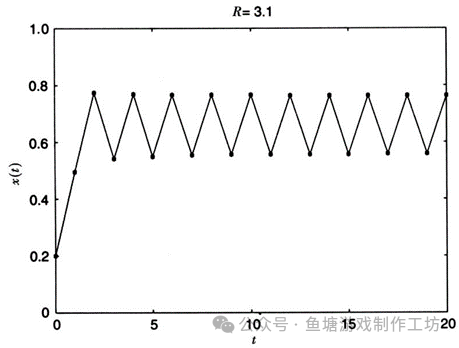
而当R=3.1时有趣的事情开始开始发生:
不管X0输入的是什么值,最终Xt都会在两个值(0.5580141和0.7645665)之间振荡。如果将前者代入方程,就会得到后者,反过来也是一样,因此振荡会一直持续下去。这种最终的变化位置(无论是不动点还是振荡)被称为“吸引子”,因为任何初始位置最终都会“被吸引到其中”。
往上一直到R等于大约3.4,逻辑斯蒂映射都会有类似的变化:在迭代一些步骤后,系统会在两个不同的值之间周期振荡(最终的振荡点由R决定)。因为是在两个值之间振荡,系统的周期为2。
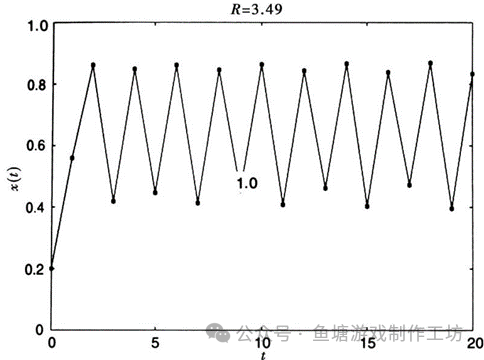
但是如果R介于3.4和3.5之间,情况又突然变了。不管x0取何值,系统最终都会形成在四个值之间的周期振荡,而不是两个。例如,如果R=3.49,x0=0.2,x的值很快就开始在四个不同的值之间周期振荡(它们分别大约是0.872,0.389,0.829和0.494)。也就是说,在3.4和3.5之间的某个R值,最终的振荡周期突然从2增到4。最终的结果就像下图那样。
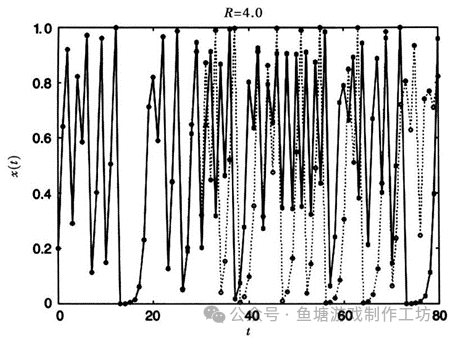
接着,更有趣的事情来了,在3.54和3.55之间的某个R值,周期再次突然倍增,一下跃升到8。在3.564和3.565之间的某个值周期跃升到16。在3.5687和3.5688之间周期又跃升到32。周期一次又一次倍增,前后R的间隔也越来越小,很快,在R大约等于3.569946时,周期已趋向于无穷。当R等于大约3.569946时,x的值不再进入振荡,它们会变成混沌。下面解释一下。将x0,x1,x2……的值组成的序列称为x的轨道。在产生混沌的R值,让两条轨道从非常接近的x0值出发,结果不会收敛到同一个不动点或周期振荡,相反它们会逐渐发散开。在R=3.569946时,发散还很慢,但如果将R设为4.0,我们就会发现轨道极为敏感地依赖于x0。我们先将x0设为0.2,对逻辑斯蒂映射进行迭代,得到一条轨道。然后细微地变动一下x0,让x0=0.2000000001,再对逻辑斯蒂映射进行迭代,得到第二条轨道。图2.14中的实心圆圈连成的实线就是第一条轨道,空心圆圈连成的虚线则是第二条轨道。
这两条轨道开始的时候很接近,但是到后面,两条轨道开始分开,并且毫不相关。这就是“对初始条件的敏感依赖性”的由来。
这就是混沌最简单的表现方式之一,只要一个公式,就能告诉我们,如此简单的逻辑斯蒂映射,并且完全是确定性的:每个xt值都有且仅有一个映射值xt+1。然而得到的混沌轨道看上去却非常随机。此外,对于产生混沌的R值,如果初始条件x0有任何的不确定性,对一定时间之后的轨道就无法再预测了。
所以,如果对于一个实际的混沌系统,即使它简单到只有一个粒子,它的初始状态中若有个参数是无理数(绝大多数数字其实是无理数,有理数只是少数),例如大家最熟悉的π,那我们就要建造一台可以输入无限位数小数的机器,否则无论我们精确到小数点后多少位,那一位后面的误差就会导致一定时间后,整个混沌系统都无法预测。这就是“失之毫厘,谬以千里”。
至此,不论从宏观上还是微观上,预测未来都不可能。
四、混沌系统和游戏
前文提到我们的游戏《流浪方舟》是应用了基于规则的复杂系统,简单描述游戏玩法,是双方玩家各控制五个球体英雄,互相碰撞进行战斗,其碰撞和反弹都是模拟的物理规则,并且有PVP的玩法。而我们游戏的机制,其实就已经组成了一个典型的N体系统(没错,N等于三就是大名鼎鼎的三体系统),也因此遇到了混沌效应。
我们用的是帧同步方案,在不同的手机上,我们遇到了两个玩家不同步的问题。排除各种原因包括网络因素后,发现原因是不同机器上的浮点数运算有微小的差异(真的非常微小)。于是,某个回合微小的差异,会在几回合后使得双方的战场情况完全不一样,直接变成各打各的了。后来,我们只能是放弃Unity自带的物理系统,自己重新实现了一个定点数精确物理系统,非常惨烈。所以,游戏利用了复杂系统,也要承受复杂系统可能带来的问题。
当然反过来说,我们也利用了复杂系统的涌现现象。对于游戏来说,涌现本身不是目的,而是涌现能为游戏带来什么。
首先,涌现能为游戏带来意料之外的体验,该部分的体验是玩家不可控的。若开发者能在这部分进行部分控制,则可以进行更多发挥。当然意料之外的体验也是新体验,涌现本身创造了新的体验。
同时,涌现的妙处在于并不是所有过程都是不可预测的,往往有一小部分是可以预测的,这会带来一定适应性,可以适应不同水平或者意愿的玩家。但是复杂系统的的突变也会带来一个相变的临界点,这个临界点又可以保证不同玩家对涌现的掌控不会相差太多。
举例我们游戏的物理碰撞系统,复杂度来自多体运动,玩家无法预测N次碰撞后的情况,但是大多数玩家是可以预测1次碰撞后的结果,这就是初始可预测部分,这部分会进入玩家的策略考量中,而对于一些更具策略的玩家,首次碰撞反弹后的第二次碰撞,也能预测部分,这就是适应性,但是当反弹三次或以上,基本没有玩家可以预料局面,这就可以类比为混沌相变的临界点,用以把控不同玩家的策略差距,甚至理论上,即使有个类似深蓝的超级计算机来算,也无法完全把控N变大后的情况。
混沌系统只是复杂系统的一个分支,但确实是一个理解复杂系统的敲门砖,大概了解了复杂系统是什么之后,我们来看看游戏与其更深的关系。
在设计复杂系统的时候,大家会发现,游戏和复杂系统的界限是非常模糊的,一个复杂系统,往往加上一些合理的目标和挑战,就是一个具备一定可玩性的游戏。而很多游戏本身,就是一个复杂系统。也因此,对复杂系统的一些研究,同样可以化用到游戏设计,例如复杂系统对“复杂度和信息”的研究,对游戏设计就非常有价值。接下来的部分章节,笔者会探讨一种度量和优化游戏的方式,若对此不感兴趣,可以跳到第八章。
五、度量“复杂”
首先我们来看看科学家们是怎么是度量复杂系统的“复杂”程度的:
1.规模度量
最简单的度量就是规模大小,但是很显然是不对的,毕竟单细胞变形虫的碱基对数量是人类的225倍。
2.香农熵
另一种直接的复杂性度量就是香农熵,香农熵定义为信息源相对于信息接收者的平均信息量或“惊奇度”。也就是说若信息高度有序,例如“A A A A A A A……A”,则熵为零。完全随机的序列则有最大可能熵。这种度量明显也是不够的,完全随机的序列对信息接受者来说也没有意义。所以最复杂的对象既不是最有序的,也不是最随机的,而是介于两者之间。
3.计算机描述
第三种度量方式是由柯尔莫哥洛夫(Andrey Kolmogorov)、查汀(Gregory Chaitin)和索罗蒙洛夫(Ray Solomonoff)分别独立提出,他们将事物的复杂性定义为能够产生对事物完整描述的最短计算机程序的长度。这被称为事物的算法信息量。对于学计算机的小伙伴应该很好理解,也就是表达一个东西需要多少代码。
例如一个游戏A最少可以用10行代码写出来,另一个游戏B却要用100行代码,那按算法信息量,游戏B就比游戏A复杂。这个乍看合理,其实也有局限,100行代码一定比10行复杂吗,代码本身的复杂度是简单的线性吗。本质上这是把系统的复杂度抽象转移到了代码上面,并没有完全解决问题,只是把系统的复杂度问题变成了代码的复杂度问题。
4.统计复杂性
第四种度量方式是物理学家克鲁奇菲尔德和卡尔·杨(Karl Young)定义的一个称为统计复杂性(statistical complexity)的量,度量用来预测系统将来的统计行为所需的系统过去行为的最小信息量。统计复杂性与香农熵相关,定义中系统被视为“消息源”,其行为以某种方式量化为离散的“消息”。对统计行为的预测需要观测系统产生的信息,然后根据信息构造系统的模型,从而让模型的行为在统计上与系统本身的行为一致。
例如,序列ACACACACAC的信息源模型可以很简单:“重复A C”;因此其统计复杂性很低。然而,与熵或算法信息量不同,对于产生序列ACGTGGTAGC的信息源也可以有很简单的模型:“随机选择A、C、G或T。”这是因为统计复杂性模型允许包含随机选择。统计复杂性的度量值是预测系统行为的最简单模型的信息量。因此,对于高度有序和随机的系统,统计复杂性的值都很低,介于两者之间的系统则具有高复杂性。
第四种度量方式不止符合直观,还有值得我们思考的是,它并不完全度量系统本身,还通过对系统演变的预测来度量系统本身的复杂度。
还有很多度量复杂性的方法,不一一赘述。各种度量都有一定可行性,但都存在的局限性,还远不能有效刻画实际系统的复杂性。度量的多样性也表明复杂性思想具有许多维度,也许无法通过单一的度量尺度来刻画。
而对于大多数系统例如游戏,并不是一成不变的,而是不断更新迭代,对未来可能性预测来反推当前的复杂度是一个有趣的方向。
六、复杂系统和游戏有效信息度
相信很多设计师在设计游戏的时候,都曾想要“度量”自己的游戏,“可玩性”,“复杂度”,“上手难度”等等,这些都是非常难以统一定义和量化的标准。我们在本文,不讨论“可玩性”这个过大的话题,只聚焦于对游戏有效内容量的探讨,有效内容量,也可以从很多个角度来侧面地衡量,例如游玩时长,系统复杂度,系统深度等等。而我们的角度不同,是从信息层面上,来度量和优化一个游戏,笔者称为“游戏有效信息度”。
游戏有多种抽象方式,其中有一种抽象就是:玩家接受信息,与游戏互动,影响游戏,游戏反馈信息的这样一个循环。信息是交互的弹药,是策略的基础材料,已知信息作为安全感来源和决策的输入,未知信息作为钩子吸引玩家探索,作为不可控因素带来变化等等。
“游戏有效信息度”就是指整个游戏系统所提供的内容,通过一定规则展现后,对于玩家预期来说,具有意义的信息量。这个信息量越大,我们可以认为游戏内容越丰富,游玩价值和可玩性往往更高。
游戏的信息丰富度当然不完全等于可玩性,但是对所有玩家或人类来说,都有不停获取新信息的欲望,同时人类又是高效的模式识别机器,当玩家熟悉特定模式和规律,一直没有新信息摄入,则会快速感到无聊。信息刺激,本身也是可玩性的重要一环。
接下来我们举个具体例子,来探讨一下有效信息度的概念:
举例,现在我们做了一个线性关卡的游戏A,每一关击败一个不同的敌人,即可去下一关,直到通关,关卡与关卡之间并没有直接的联系。
假设我们制作了一系列的关卡内容,例如10关,我们预期这些关卡玩家会游玩一次,通关后不再想玩,我们先假定,这个游戏的有效信息度为10。
以此为前提,有几个有趣的问题:
问题1
这时候,加入一个设定,通关后所有关卡会打乱,假设我们预期玩家会因为这个设定再通关一次,耗费了玩家双倍的时间。
那这个游戏的有效信息度会变成20吗?
如果不是,那是更偏向10还是偏向20?
问题1探讨
很显然,不是20,重点就是有效信息度不等于游玩时长,而是玩家对内容的感知,能接受到的有意义的信息量,而关卡若只是打乱随机,对于玩家游玩来说,关卡信息并没有变化,换句话来说没有新的信息给到玩家,也就没有新的体验。所以问题1的游戏有效信息度应该是接近并略大于10的一个值。注意,我们在此并不关心有效信息度的绝对精准值(也无法做到完全精准),我们只需要尽量定量,并且通过对比分析等方式逼近实际值即可。这个问题也呼应了复杂系统复杂度的度量,纯随机和纯秩序,复杂度都很低。(所以优秀rogue的重玩性并不是只来自随机)
问题2
在问题1 的讨论我们已经知道,游玩时长和次数是结果,并不等于有效信息度。在这个基础上,所有关卡打乱后,让玩家可以一直重复游玩,每次游玩的关卡顺序都会变化,那游玩价值又有什么变化?
问题2探讨
本质上消耗的是顺序不同带来的体验价值
和前面的信息呼应,纯随机和纯秩序都是信息量较低的状态,也就是游玩价值不会很高
同时,讨论线性和非线性系统也有额外的意义,若关卡间的关联小,则先A后B还是先B后A并没有本质区别,而若关卡间是非线性地互相影响,则顺序本身就被赋予了意义,或者说被赋予了额外信息和复杂度,则可能产生更多的有效信息度。所以重点不在于关卡打乱的随机,而是在于关卡间的关联设计,是否赋予这个随机足够的意义。
问题3
在原方案基础上,多做了1关,并且设定为通关一次后,再次通关才可以玩到这个额外的关卡。
假设每个玩家都因为这个设定,重新通关一次,那此时这个游戏的有效信息度大约是多少?
和直接放出11关给玩家的区别是什么?
问题3探讨
和问题1的探讨类似,也许这个游戏的游玩时长的度量接近翻倍,但有效信息度只是接近11左右,这意味着,玩家在近翻倍的体验时间中,体验的质量其实是有所下降。其实和直接放出11关给玩家没有本质的区别。那么为什么还有很多游戏会使用这个技巧来延长游玩时间呢?其实是来源于除了上述游戏机制本身之外带来的可重玩性,类似问题2讨论的非线性关卡,这些额外的因素,使得游戏的有效信息度在其他维度得到了提升,所以不属于问题3的讨论范畴。这个例子想要说明的是,有效信息度的分析一定要客观剥离其他因素,否则将失去参考价值。
问题4
还是这个线性关卡的游戏,什么都没变,但是给与一个额外目标,通关时间,然后允许玩家重玩,游戏有效信息度又如何?
问题4探讨
这个问题,理论上有效信息度相对于原方案并没有太大变化,但是我们直观会认为,相比原方案,该方案更具可玩性。这个问题想要说明的是,技巧挑战等内在驱动力,会为相近有效信息度的游戏,带来较为不同的可玩程度。这也是证明游戏有效信息度并不完全等于可玩性的例子。
问题5
基于问题4的额外通关时间目标的设计,更进一步探讨,若是游戏中原本就有一个道具,本来强度一般,但对速通有帮助。因此,玩家在没有通关时间目标时,和有通关目标时间时,有效信息度的变化?
问题5探讨
我们可以看到,除了目标的变化,其他都没有区别,理论上,信息量完全没有差别。但是实际上很显然,后者有效信息度一定大于前者。这就是“有效信息度”定义里的“有效”的意义:一份信息,通过机制,转化为对可玩性有意义的信息后,才能称为有效信息。具体见下一章的探讨。
经过上面几个问题,大家应该可以理解游戏有效信息度的意义,它虽然不等于可玩性,但是是对一定时间内,玩家体验的丰富有效程度的一个度量。它尤其能帮助我们思考时摒弃无效游玩时长的陷阱,并在一定程度上帮助我们对比衡量游戏设计优劣。
七、有效信息度与游戏设计
有效信息度如何切实帮助设计?我们应该如何看待,操作游戏中的信息?
玩家游玩游戏的过程可以视作一个接受信息,处理信息,获得信息反馈的过程。设计师提供一系列的信息给与玩家处理,玩家在处理这些信息的时候,通过自身的操作和策略等,收获不同的反馈。对于一个玩法,持续有节奏地给与玩家适量的,有意义的新信息让玩家舒服地处理,则从信息角度来说是一个好的玩法。
游戏的信息不是全部一次性释放给玩家的,一个游戏的信息有很多种维度,例如规则信息,游戏世界环境的信息,关卡以及挑战的信息,反馈及收获的信息等等。玩家的目标挑战反馈循环中,每个环节都在不停释放新的信息。而新的信息的意义是什么?是产生新的变化。
但是,如前文所说,一份新的信息,产生的变化往往不是一份新的游玩体验,而我们的目标,就是让一份信息,产生十份变化,最终转化成两份可玩性。
有限的内容下,如何规划这些信息将是关键。直接说几种方法:
1、规则辅助对手产生新信息
拿棋类游戏-象棋举例,象棋所有规则信息,是不多的。而战场环境信息(当前棋盘情况)是千变万化的,我们很容易得知道,象棋不是靠规则信息的逐步释放来产生变化,同时象棋又不带任何随机性,所以是个很好的例子,帮我们聚焦到这一方式——规则辅助人产生信息。
人人间动态的博弈,带来持续可玩性,不是什么神秘的事情,但在信息角度,其实是有要求的,人产生有意义的内容,需要规则进行引导,什么叫引导?例如象棋里对所有棋子移动方式的限制,就是一种引导,这些限制使得玩家能够部分预料下一步对方会如何行动,从而结合场面,最终给与当前回合玩家,一个正在不停变化但又有决策参考意义的信息,这个信息将会结合对方玩家的行棋风格,水平等因素,产生多局之间的变化。
一个好的机制或者说规则,告诉玩家能做什么是基本,更重要的是约束玩家不能做什么,将无限的选择空间压缩到合理范围且不策略收敛,并且让对手每个选择反馈出新的信息,例如,单步中没有明显的最优解,那是防守还是激进换子,其实暗藏对手风格信息,这个信息,是基于规则但超越规则的额外信息收益。
2、辅助玩家自身产生新信息
我们可以把游戏抽象成目标挑战反馈三者循环,整体游戏由无数个大小循环嵌套组成。从信息角度我们可以有新的视角看待这个循环,每个部分都能通过设计辅助玩家产生新的有效信息。
对于目标,往往是最明确简单的信息,对于单个循环一般不会刻意藏匿目标的信息,因为对于设计来说,单个循环目标越明确越清晰越好。但整体上,目标可以有多个,可以逐步释放,可以引导玩家自身赋予目标,有非常大的操作空间,目标往往是一切的起点,会成倍放大其他信息的效果。
最好的方式,就是刺激玩家自己赋予自己目标,例如沙盒游戏,通过包装世界观等信息,让玩家想要爬上那个跟任务无关的山顶,想要拯救某个无关紧要的村民。设计师提供的信息作为外因驱动作为引导,玩家自发产生的目标作为强大的内因驱动。
对于挑战,分为挑战本身和玩家克服挑战的过程,例如策略和操作。对于这部分信息的自发产生,来自挑战本身需要提供足够高的适应性,使得玩家自身情况的不同,能在挑战和克服挑战的过程中体现出来。同时要足够敏感,玩家细微的变化,最好都要所体现。
举个例子,完成挑战的方式有多种倾向,玩家根据自身喜好,能力,选择其中一个方式进行挑战,此时,玩家所有的操作和策略,将会产生基于自身的独一无二的信息。
对于反馈,这里重点不在给与玩家的反馈,而在于完成挑战后给与系统的反馈,重点在于前后不同挑战间的关联变化,也就是说,需要配合上述挑战部分,玩家做出的细微区别,反馈需要让系统对接下来的挑战产生足够影响,就会产生指数增加的变化。如此配合,也是涌现的一种设计方式。(具体后面章节细说)
3、促进多人之间产生互动
和第一点本质一样,稍有区别,留作思考题吧哈哈,分析麻将和双人棋类间的区别即可。感兴趣的朋友可以参考笔者的麻将相关的文章:https://mp.weixin.qq.com/s/RUFNdkrFy8e2oqEhsYp_Xg
4、逐步释放和重组信息
玩家自发发现信息,而不是设计师塞给玩家,发现的过程本身是一种有意义的获得行为,会丰满整个游戏。这是一种较好的逐步释放信息方法。
巧妙地重组信息,来重用信息。这点比较好理解,就不赘述了。
八、复杂系统与涌现应用
上面的章节简单介绍了一下复杂系统以及和游戏的一些关联,由复杂系统启发,提出了一个游戏度量方面的不成熟想法,抛砖引玉。接下来的章节将会以实际的原型设计为案例,来深入探讨一下复杂系统和涌现设计在游戏设计中的应用。
思维实验
第一步我们先来做一个思维实验,前文介绍过,现实世界就有很多复杂系统,我们不妨试着挑选现实中的某个复杂系统,假设我们是全能的计算机之神(狗头),已经把这个系统百分百实现出来了,同时,作为设计师,我们知道,拟真不等于好玩,那现在,我们需要思考一下这个系统中不好玩的东西是什么,去掉,好玩的东西是什么,强化。再添加一点佐料,加入一点目标,设置一些挑战,给与足够的反馈,这个时候,相信我们的脑海里已经有一个也许简陋,但也能成立的游戏了。
对现实的抽象和剪裁过程尤为重要,我们会逐步抽丝剥茧,把不重要的外在去掉,看到涌现的核心,来随便举个例子。
假设我们取现实中的经济系统作为我们的复杂系统,我们先赋予一个简单的目标,就是赚得多少金钱。然后我们刨除掉一些冗余的东西,最终可能剩下这么一个系统:
系统中有若干个经济理性人,包含玩家在内,他们会想办法以最小的代价去获得最大的利益,这些决策实体我们统称为“代理(agent)”——代理(agent)是一个计算机,人工智能和经济学领域的术语,指的是接受信息,进行决策,执行行为的主体,可以是人,AI,组织,一段程序等等。在这个过程中,代理们会和其他代理,和环境进行交互,进行时间,信息,资源,收益的不停交换。想象一下,当这个系统运转起来,我们在这个系统中的获得的乐趣来源于什么?与一个普通的交易模拟游戏的差别在哪里?
这个简单的系统抛开声光电反馈等冗余外在,我们可以发现,玩家的核心策略是收集信息,根据信息做出自己收益最大化的决策,自身的决策又会影响整个系统,系统改变其他代理的行为决策,每个代理的行为都相当简单,但整体上会涌现出很多有趣的现象,例如哄抢,垄断,通胀通缩等等现象,使得挑战/问题/谜题动态变化,像是多只蜘蛛在弹奏同一张蛛网。
以上,这个复杂系统在提供有意义的变化,产生新的可玩内容,这是重玩性的根本。同时,由于玩家对环境的影响足够深远,反馈会更强。
让我们再对这个游戏加点料,假如这个游戏加入了另一个玩家,双方有同样的目标,这时候我们很容易发现一点,复杂系统不可控的部分,正在平衡优劣势,拉近不同水平玩家距离,同时部分降低操作和策略门槛。
更进一步,我们会发现,就类似于现实的经济系统,我们这个简陋的复杂系统本身就是一个自适应系统,有时候像海绵,吸收玩家和代理们的重大行为,减小影响,有时候又像喇叭,放大一些微小的噪音。而在这个时候,我们如果再为这个简化版的经济系统加入一些引导性的设计,例如价格和资源消耗的调控(类似央行和美联储),可以去操控它的海绵或者喇叭,达成改变和控制游戏节奏的目的。
再进一步,我们不满足于单个目标,若是我们加入了多个胜利条件,我们会发现,基于复杂系统本身的多目标,更好设计,更能满足不同类型玩家的游玩需求。
最后一步,让我们把对方玩家又去掉,把玩家会进行的一些行为和代理的行为进行比较,把一些简单的,玩家会额外进行的侵略性较强的行为,或是非理性的行为,赋予代理。并且把和玩家的对抗的目标改为和代理对抗,我们就会发现,相对于其他游戏,在玩家感知中,代理会更接近真实玩家。
当玩家面对一个整体的复杂系统,去对抗其中的一些代理时,要比对抗某一个NPC时,对系统智能的评价更高。因为玩家对一个客体的智能的评价,除了智能行为本身,还由很多和智能不相关的因素组成,例如外观,强度,数量,环境等等。例如光环设计师在GDC分享过的一点,只是单纯的增加敌人的强度不改变AI,玩家对敌人的智能评价就会更高。例如帕鲁正因为远离人的形象,玩家对其智能期望低,反而觉得其智能表现不错。复杂系统的不可控和可解释是一种更好的“难度放大器”,同时,复杂系统放大行为的反馈同样适用于代理,这就是在解释和掩盖一些非智能行为。
通过以上这个思维实验,我们可以大致总结一下复杂系统和涌现的优势,同时也是我们设计他们的目的:
- 产生有意义的变化,来提供新的体验
- 增强玩家对环境的影响与反馈
- 平衡优劣势,拉近不同水平玩家距离,降低操作和策略门槛
- 改变和控制节奏
- 承载不同类型玩家的游玩需求
- 部分替代其他玩家的作用
以上思维实验中,每位朋友选取的复杂系统可能都不一样,但当我们多思考几个复杂系统,将真实世界抽象的过程中,我们会发现,复杂系统和涌现可以分为两个偏向:
- 以代理(人,动物,AI等)为核心的复杂系统,例如蚁群,公司,社会,经济系统等。
- 以客观规则为核心的复杂系统,例如基于物理化学规律的湍流,天气,N体运动等。
当然两者混合也是一类,这里不讨论,只探讨这两大类,这两大类核心区别当然就是代理主体的存在与否。对于游戏来说,这两个偏向的设计方式相差非常大,第一类代理为核心的游戏有模拟人生,SLG等等,而我的世界,noita,以及我们自己的游戏流浪方舟,更偏向第二类。
接下来,我们会通过七个玩法原型,一一来窥探涌现设计的一些精华。这些都是纸面原型,只需要简单的纸笔,或者一些简单的道具例如骰子就可以实现,感兴趣的朋友可以跟着做出来玩一玩,会有更深的理解。如果对设计不感兴趣的朋友,可以直接跳到第十六章结论和探讨部分。
九、原型1随机平替涌现
1.1设计目的
原型要求
- 尽量简单的规则,只利用单纯的数字,加减法
- 能够成立的基础博弈,不会发生策略收敛
- 能够提供一定的策略深度,拉开不同玩家之间的差距
- 有随机性的空间,用随机来模拟涌现
- 能够展现重玩性,优劣势平衡等特征
随机和涌现的异同:
- 由于一个由确定性导出混沌,另一个由随机性导出混沌,对于玩家的感知来说,前者的掌控程度远大于后者,也就是说,玩家会更觉得涌现的结果和自己的决策或者输入相关。同时,玩家对于两者发生结果的归因会有差异,随机性的结果玩家会更归因于系统,涌现若是设计的好,玩家会更归因于自身。这个特性,是涌现优于随机性非常重要的一点,也对游戏设计有非常重要的意义。
- 第一点是感知上的掌控程度,而实际上,对于玩家来说,涌现部分理论上也是可掌控的,对不同情况的玩家适应性会更强。
- 两者从确定到不确定的起始节点,是完全不同的,随机*随机,某一层随机,往往就是混沌的起点,相对离散,而涌现则连续很多,这一点对设计也很有意义。
- 涌现是确定性的,就像前文展示的逻辑斯谛方程一样,每一步迭代都是确定的,可计算的,只是超过计算能力的部分,对于计算者来说,就是混沌不可预料的。
- 对于随机来说,即使不同随机结果的概率已知,对于计算者来说,仍旧是不可控的结果,若叠加了很多重随机,也就是我们常说的随机*随机,这个时候更容易出现对于概率预期不清,于是完全放弃这部分计算,变成混沌不可预料,对于这部分,随机和涌现在结果上有相似之处。
然而,两者的混沌部分,仍旧有几个非常重要的区别:
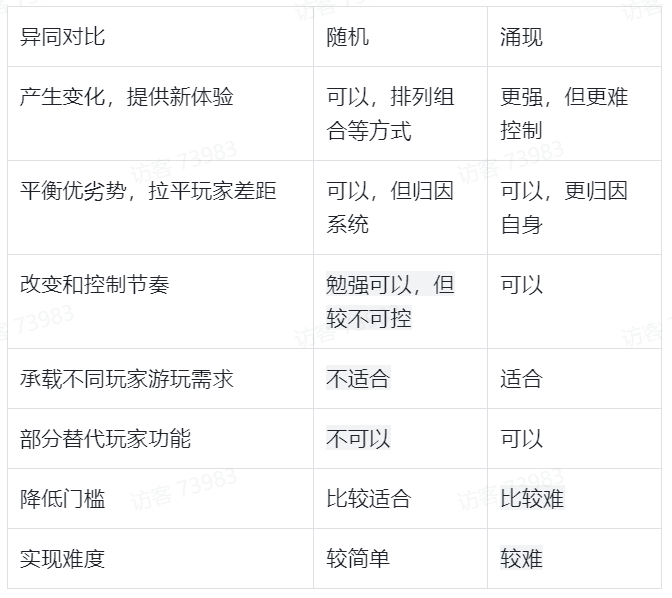
还有一些异同,总结在下表中:
综上,由于随机和涌现在不可控部分,有一定相似的特征,并且随机的实现难度远小于涌现,所以原型一般先用随机来平替涌现,来验证可行性。
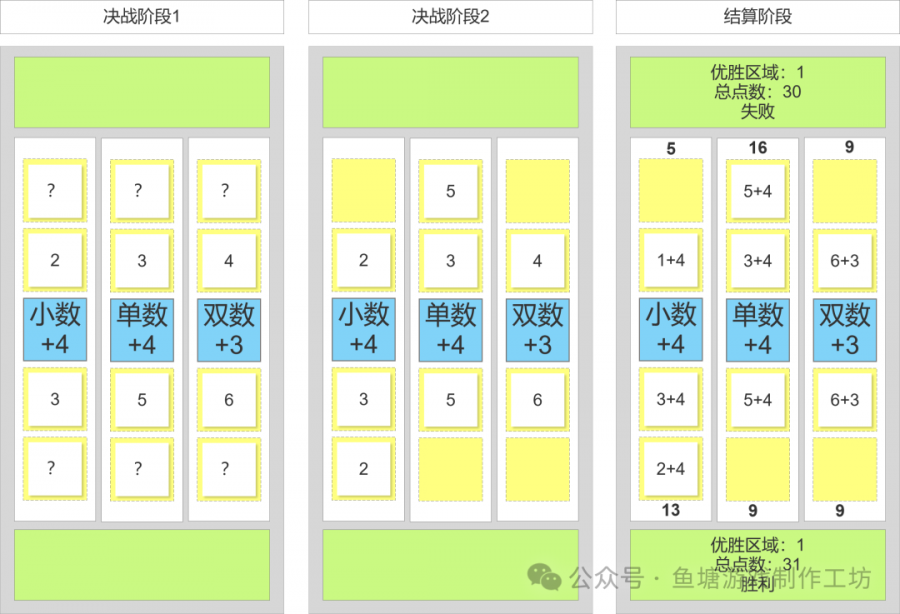
1.2玩法规则
玩法概述
双人游玩,有三个战场,每个玩家四张手牌,共四个回合,每回合双方放一张手牌到战场,最终结算点数,三个战场中获胜占领两个以上的玩家获胜,平局按点数分胜负。
回合阶段:
- 双方各从6张1——6的数字牌中随机抽取4张牌
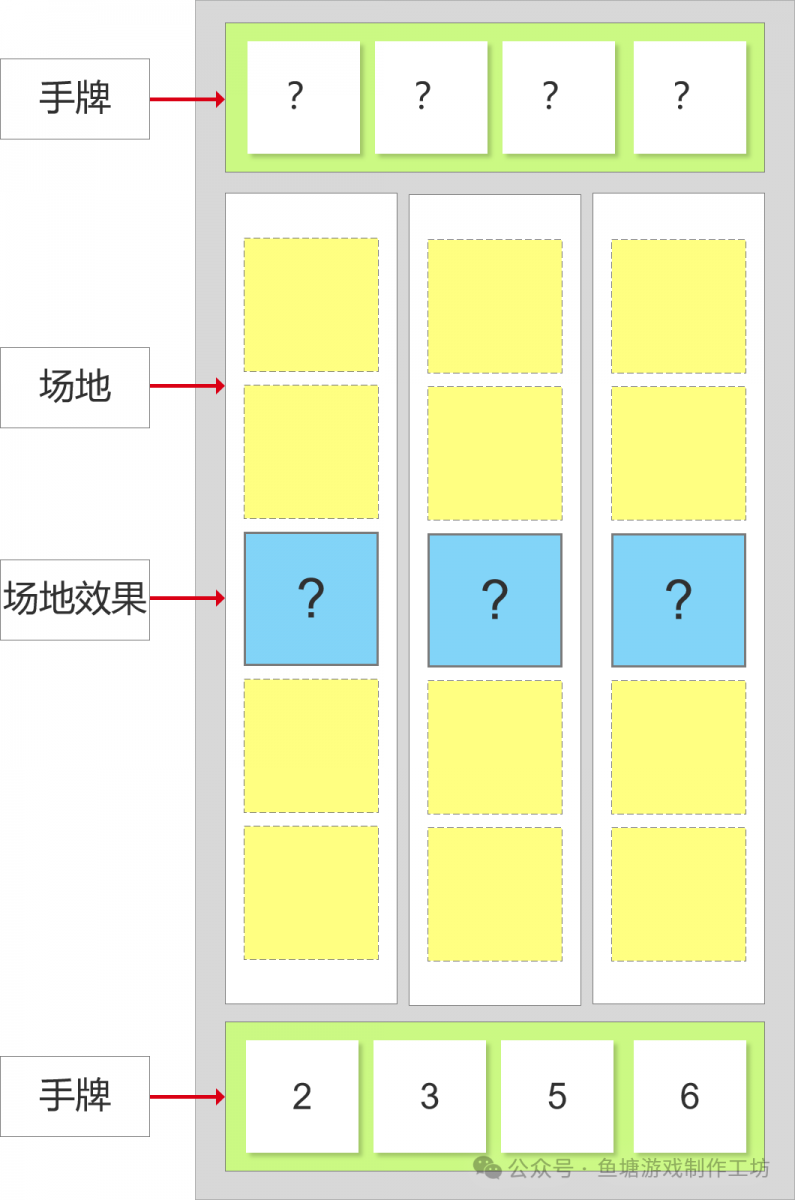
- 从5种场地效果中随机抽取3个场地效果,先不揭示
- 揭示第1个场地效果,双方各自选择放入一张手牌在该战场,背面朝上,然后揭示
- 重复上述,直到3个战场各放置3张牌
- 第4回合,双方将剩下的最后一张牌放在任意战场,双方不知道对方放置情况(拿两张无用牌掩盖)
- 揭示最后一张牌,结算结果
结算阶段
优胜场地数量相同,则比较总点数,总点数高的玩家胜利
总点数相同,则视为平局
例如场地内是1和2,场地效果是[小于等于3的数+1],则最终变为2和3
- 根据场地效果对每个数字单独进行修正
- 对比每个场地内双方的卡牌点数总和
- 总和较大的一方获得该场地的优胜,一样则平
- 优胜场地较多的玩家取得胜利
5个场地效果
- 单数卡片结果+4
- 双数卡片结果+3
- 大于等于4的卡片结果+1
- 小于等于3的卡片结果+4
- 投六面骰,投中点数在该战场视为7
1.3设计思路
基础
- 用简单的数字创造1个原型玩法
- 最小玩法为双方各出1个数字比大小,大者胜
加入策略对抗和策略深度
- 第1层:引入3局2胜的上校博弈,考验玩家的资源分配能力
- 第2层:加入第4张牌,第4张牌可以作为关键牌逆转局势,也可用来诈唬,考验玩家的博弈能力
- 两层策略相乘,创造出足够的策略深度
随机和对抗随机
- 通过资源分配对抗随机
- 通过推理对抗随机
- 通过博弈对抗随机
- 考虑场地效果的后续可能性去进行资源分配,对抗场地效果的随机性
- 根据对方前3张牌,推理对方最后1张牌的数字,对抗对方手牌的随机性
- 在牌处在劣势的情况下,制定高风险高收益的策略,进行诈唬和偷鸡,对抗我方手牌的随机性
- 第2轮随机,随机范围小,两层小随机只是承载一点重玩性和策略拉差,不加入过多策略负担
- 通过场地效果拉平各数字的价值,对抗第1轮随机,降低随机手牌对胜负的影响,防止策略收敛
- 与第一轮随机同理,揭示第1个效果后,后续只有6种组合,揭示第2个效果后,最后1个场地只有3个选项,玩家只需要在个位数的选项中,决定自己的资源分配策略
- [双数+3],[单数+4],单数额外+1,保证单双数价值相同
- [大数+1],[小数+4],小数比大数的加成多3点,拉近大小数价值
- 随机1个数字变为7,第3轮小随机,提升废牌(吃不上其他场地效果的牌)的价值,为玩家提供翻盘或诈唬的可能
- 第1轮随机,随机范围小,限制了不可控的部分
- 决战阶段,对方最后一张牌只有3种选项,玩家根据3个选项进行推理即可
- 保证任何拿法,一方一定有至少一张单数双数,至少一张小牌和大牌
- 卡牌6随4
- 场地效果5随3
- 玩家对随机的对抗
1.4与扑克的对比优化
原型1已经以比较优雅简洁的方式实现了一个随机替代涌现的方案,但是仍有不足之处,我们拿扑克来进行对比:
信息暴露密度
- 优化:在翻地阶段双方轮流出牌,降低暴露密度,后手玩家可根据先手玩家出的牌和场地效果去出牌,降低了后手玩家的推理量,后手玩家在翻地阶段取得了信息上的优势,需要平衡双方的优劣势,可以在决战阶段,要求后手玩家先出牌并揭示卡牌所在场地,让先手玩家在决战阶段获得信息优势
- 但上述的优化会引入先后手问题。
- 扑克的信息暴露频次高,信息量较小,每翻1次牌,每加1次注就暴露一层信息,且前后关系联系紧密,方便玩家进行推理,负担较低。
- 原型1的信息暴露频次低,但信息量较大,每次翻2张牌,分析量翻倍,且需要通过全局的卡牌和地牌进行推理,负担较高。
信息可控程度和信息范围
- 优化:随机场地效果后,直接揭示全部场地效果,或先揭示前2张,降低不可控的信息。
- 但是加入加注设定后,不揭示场地效果更好。
- 扑克的河牌是已知的,不可控的信息是对方的2张手牌,且玩家数量会越来越少,不可控的信息会逐渐减少
- 原型1中玩家有4张卡牌,对方的卡牌与卡牌分配策略,对于玩家来说是不可控的信息,相对扑克数量翻倍,但因为只有1——6,信息范围会相对减少
- 原型1中还有3张场地效果,场地效果陆续揭示,在未揭示之前,这也是一部分不可控的信息
胜利条件
- 扑克胜利条件简单,用卡牌花色和数字进行大小对比,玩家很容易处理
- 原型1的胜利条件,涉及到优胜区域计算和点数计算,玩家不容易处理
1.5原型1总结
原型1通过非常简单的规则,已经具备一定的可玩性和深度,同时具有重玩性。同时用两道非常受控的随机来模拟涌现,已经可以感受出前述的两个特性:
- 产生有意义的变化,来提供新的体验。
- 平衡优劣势,拉近不同水平玩家距离,降低操作和策略门槛。
这是一个很简单的原型,主要是展示怎么用随机来平替涌现,以及涌现在游戏中的大致感受,我们还可以以这个原型为基础,不断拓展规则,例如加入扑克下注的玩法:
只需加入一个规则,前三回合,玩家可以在每一轮揭示战场上的牌之后,点数大的一方进行下注,对方必须跟注才能继续下一轮。同时一方也可以随时放弃,另一方拿走所有筹码。
如此设计,在原先的策略基础上加入了心理博弈,更发挥出每回合信息暴露的策略乐趣,提高策略上限。
原型1是一个简单的基于规则涌现的设计展现,接下来会从抽象即时战斗的原型开始,逐步探索基于代理的涌现设计。
十、原型2即时战斗抽象
2.1设计目的
我们来尝试抽象一场典型的即时制战斗,先将战斗简化为1v1的两个玩家,各操控一个单位,胜利目标是击杀对方单位。其他各种衍生玩法都可以视作该单局最小战斗的变种。进一步抽象,玩家是在调配战场中的所有资源,达成战胜敌方的目的,将敌我双方的所有资源分为如下几个类型:
- 直接关联胜负的生存能力,例如血量,续航等
- 直接关联胜负的输出能力,直接间接伤害,限制敌方续航等等
- 直接关联胜负的生存输出能力变体,例如机动性,限制敌方机动性的能力(同时包含生存和输出能力)
- 前三个能力的间接版本,例如召唤物或环境的各项能力或者是他们赋予关键单位的能力
和之前的原型一样,我们要用最简单的规则,只用数字的加减,来模拟这个战斗模型,这个原型同样要达成以下几个目的:
- 能成立的基础策略博弈
- 对即时制1v1战斗有足够准确的抽象表达,尤其是和战斗策略紧密相关的属性,比如机动力
- 足够健壮,适合拓展,作为后续涌现设计的基础
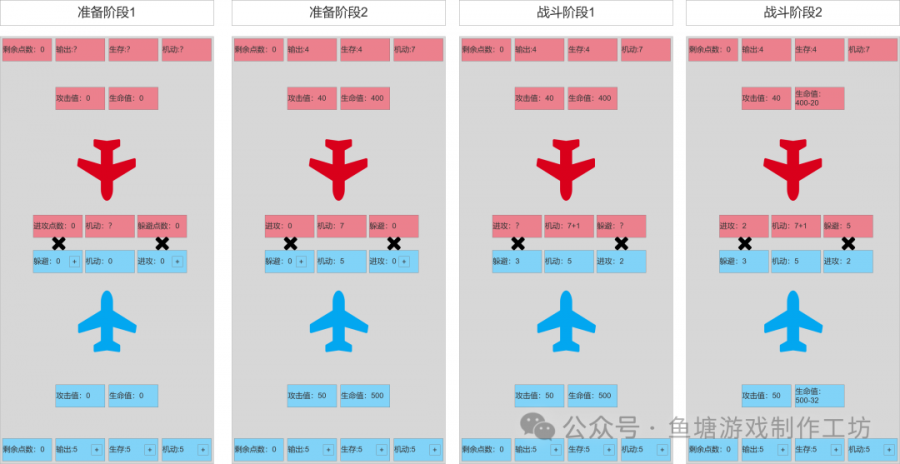
2.2玩法规则
玩法概述
双人对战,玩家将资源投入到输出/生存/机动属性上,机动属性可再进行一次分配,分配到[进攻]和[躲避]上,双方互相攻击,造成的伤害由玩家分配的资源情况决定,血量先归0者失败
玩法流程
受击方[躲避点数]与进攻方[进攻点数]对比,每高1点,进攻方造成的伤害减少20%,至多减少100%,没有进攻高,则进攻方造成伤害不变
- 将15点基础点数分配到各自战斗单位的输出/生存/机动属性上,然后公示分配情况
- 将输出属性*10作为战斗单位的攻击值,将生存属性*100作为战斗单位的生命值(非必要,为了计算简单,减少小数计算)
- 每回合战斗开始时,将机动属性上的基础点数进行1次分配(机动属性高的一方可额外获得1个点数),分配至[进攻]行为和[躲避]行为上,然后公示分配情况
- 高机动属性的一方先进行攻击,根据攻击值对对方造成1次伤害,伤害需要根据双方行为点数进行1次修正
- 双方攻击结束后,没有单位血量归0,则从步骤3重新开始,有单位血量归0,结束战斗
2.3设计思路
先采用最小单位,两个战斗单位互相攻击
用离散的回合来模拟即时,更直指本质
将战斗单位的优劣势抽象成3个维度,输出/生存/机动
引入点数,玩家需要分配点数到3个维度中,用简单的数字进行战斗模拟
- 机动能力高,则输出/生存能力就会降低
- 第一轮分配,通过限制点数的总和,模拟了机动能力对输出/生存能力的影响
第一轮分配结束后,输出和生存点数固定,机动点数可再进行分配
- 机动能力可用于追击对方,提升输出能力
- 机动能力可用于躲避攻击,提高生存能力
- 机动点数稍微比对面高,则在每轮的攻击中占据优势,但高于一定值后,将不再获得收益
- 机动点数的再分配影响战斗单位的伤害,再次模拟机动能力对生存/输出能力的影响
- 机动点数的再分配,每一轮战斗都允许不一样,模拟了机动能力的转化能力
2.4原型2多V多拓展
可以很简单的将原型2拓展到多VS多的规则:
额外多一个目标选择阶段,机动力低的单位先开始选择(相等时随机),选定目标后本回合不能改变
目标选择完成后,进入机动性分配阶段,规则有所补充:
机动性的进攻点数,只能分配给该单位之前选的目标,而躲避点数,可以分配给所有以该单位为目标的敌方
但是,每多分配一个目标,机动性额外消耗1
所有单位分配完机动性,则开始战斗
战斗结算顺序,所有同时结算即可
结算时规则和基础战斗规则一致
2.5原型2总结
通过让玩家在战斗中将有限的资源进行分配,体现出了机动能力的两个特性
- 可自由转化成输出/生存能力,对输出/生存能力产生影响
- 当机动能力高于敌方过多时,将反而变成劣势
在原型2可很简单的拓展至1对多和多对多的玩法,进一步模拟复杂战场上的情况,初步证明了原型2的拓展性较强
资源分配的还能体现出对战游戏中的一些设计思路
- MOBA游戏中的行动指令(移动、攻击、释放技能)
- 回合制游戏中的行动指令(攻击、防守、释放技能)
- 卡牌游戏中的行动费用
- 而在设计战斗单位风格时,也是对这3个方面进行资源分配
- 可留有一定的空间让玩家进行分配,比如说加入天赋系统和养成系统
- 战斗单位的所有优劣势都可抽象成输出/生存/机动3方面
- 在战中可进行再分配的机动属性,为玩家在局中创造出了策略空间,让玩家去自主的进行变化,创造不同的游戏内容
原型2策略博弈分为两层,一层为开始的三个初始战斗资源分配,一层为战斗中机动力的使用,这两层策略和对方的信息关系都不大,更偏心理博弈,单看这个原型策略深度不够,但作为后续原型的基础是足够的。
十一、原型3抢占资源
3.1设计目的
到这一步,我们有了一场基本战斗的抽象,在原型3之前,我们先将原型1的思路融入原型2,再次从另一个角度分析一下涌现
玩家已有单位间的变化,与玩家变化统一,并且互相影响,则抽象为:
玩家在削弱敌方玩家的生存,输出和机动能力,最终目标是生存能力归零
同时,玩家防御敌方对自身这三种能力的削弱
在以上过程中,对环境产生影响,并受到环境的反馈
环境的反馈可能有益于我方或敌方,并且分为可控和涌现部分
1可控的部分
- 玩家有意识追求有利于自身的可控部分,需要尽量简单并控制数量,因为环境本身需要尽量对双方都公平
- 这部分真正的目的是刺激玩家与环境的交互,来作为涌现的触发器
- 例如玩家为了摘苹果砍树,树倒了砸中玩家或敌方玩家
- 值得注意的是,可控部分对于双方玩家最好是一致的设计,因玩家的各种差异而自然分出有益与否,降低信息复杂度
2涌现的部分
- 不可控部分,有益于敌方还是我方没有区别,但是设计上,倾向于有益我方的可控部分引出的涌现,是同样有益于我方的
- 同时,涌现的部分,玩家不是完全不可控,而是掌控程度较低,与可控部分是一个渐进变化的过程,同样作为玩法上限
- 最后,涌现部分需要设计师尽量可控,例如倾向于帮助弱势的玩家等等,但是需要尽量让玩家觉得合理
忽视原型2,我们从头抽象一个符合我们玩法的最小模型来实现上述理论:
- 最简的不可控部分用随机数进行表达,数字越大优势越大
- 最简的可控部分与核心机制保持一致
- 将玩家的能力抽象为三部分,输出能力,生存能力,机动能力,用数字表达
- 机动能力高的一方有优势,但是边际效益快速递减
- 机动能力本身有其作用,同时对生存和输出能力有加成
战斗开始时双方自由分配9点点数到三大能力上
战斗开始时,根据分配到机动性上的点数M进行随机1-M,双方较大的一方额外加1
双方可以将最终的点数M自由分配到输出能力和生存能力上,作为临时输出和临时生存
双方互相用自身的输出对对方的生存造成伤害,优先扣除临时生存,回合结束,清空临时输出和生存
循环回合,生存能力先归零的一方失败。
接着我们将涌现抽象为:
临时加成,永久加成,临时代价,永久代价
自选风险,高风险高收益
考验类,输出or生存or机动性大于等于N时,获得加成X
临时代价以及临时加成类,输出or生存or机动性临时减X,临时获得加成X
永久代价永久加成类,输出or生存or机动性永久减X,永久获得加成X
最后我们将涌现拆分为几个部分:
- 玩家可控交互部分,包含玩家可控的交互,涌现系统给与的反馈。玩家能够给与涌现系统的有a资源信息,当前/最大/基础/临时的输出,生存,机动能力的数值信息;b资源本身,消耗或变化输出,生存,机动能力本身;c玩家的选择或操作交互。
- 可控交互部分对涌现系统的影响,涌现系统的自组织。涌现系统本身内部的逻辑需要支持获取外界的信息,并且在内部进行交换。
- 涌现系统自发进行的变化,对玩家产生的反馈。
基于以上的分析,我们来看看原型3的实际规则:
3.2玩法概述
基于原型2的基础战斗,改为每个回合都会产生三个临时属性,临时攻击,临时生命,临时机动力
每个回合依次出现三个随机资源,双方投入自己的三种临时属性进行争夺,竞价模式
争夺完三个资源后,使用剩余的临时属性进行基础战斗
3.3具体规则
- 战斗开始时双方自由分配N点属性到攻击,生命,机动力上,这三个属于永久基础属性,同时揭示结果
- 从若干种资源中随机抽取三个资源放在场上,不揭示
- 每个回合开始时,揭示一个资源,并根据当前基础属性,产生对应点数的三种临时资源
- 双方开始竞价争夺这个资源,一方可以出价N点临时属性,另一方可以选择大于对方点数的临时属性,或者放弃,以此类推
- 获得资源的一方,即时触发资源的效果,完成触发结算资源后,进行下一回合。
- 当三个资源都争夺完成后,双方用当前的临时资源进行一轮战斗,战斗规则和原型2一致,额外的,超过临时生命的伤害扣到基础生命属性上。
资源具体效果
6张资源消耗卡,临时攻击/生命/机动,永久攻击/生命/机动
6张资源获得卡,临时攻击/生命/机动,永久攻击/生命/机动
每次随机资源效果时,从消耗卡和获得卡中,各随机抽取一张,组成该次资源的效果
每种组合有不同结算效果,具体如下:
1.消耗临时XX,获得临时XX
玩家自己选择1-10的N点消耗的代价,N不能大于自身拥有的点数
投一个10面骰子,点数需要大于等于N才成功,成功后收获是代价的2倍,失败代价不返还
举例:
抽到了消耗临时攻击,获得临时机动,这时候玩家有6点临时攻击
玩家可以选择1-6的消耗,例如选了5点,则投10面骰子,大于等于5,则判定成功
该玩家扣除5点临时攻击,并且获得了10点临时机动,反之,则扣除5点临时攻击,什么也没获得。
2.永久换临时
玩家自己选择1-10的N点永久代价(扣除基础属性),N不能大于自身拥有的点数
10面骰子需要大于N才成功,成功后收获是代价的5倍,失败代价不返还
3.临时换永久
玩家换1点永久资源,玩家有N点该临时资源,10面骰结果小于等于N才成功
例如该玩家抽到了临时生命换永久生命,该玩家有7点临时生命,则10面骰投中小于等于7就会获得1点固定生命
该临时资源只用于判定,不会消耗
4.永久换永久
固定1点资源换2点永久资源
不需要判定,直接消耗1点对应资源,换取2点目标资源
3.4设计思路
- 该原型模拟的实际情境是,若是引入环境的涌现因素,玩家某一段时间片段内,其实是会将这段时间的临时资源投入到环境优势的获取上,例如经典的野怪,河道buff,或者是占据一个优势地形。这些战中的优势,其实都需要玩家拿一定资源进行交换,比如玩家移动到一个优势地形,其实就是拿一部分机动力换取地形优势,地形优势如果是加防御,其实就是我们的临时机动力换临时生命。其他同理,所有战中不直接和敌方进行战损交换的行为,都可以用这个原型进行抽象表达。
- 同时,该原型的目标之一是用极简的方式来实现涌现的适应性,尤其是对战局优劣势变化的适应性。
- 引入玩家对抗不可控的体验,通过让玩家自由选择风险回报策略
- 同时玩家的决策通过随机性,间接地影响系统的结果以及接下来的战局,部分模拟涌现的过程
- 用一个10面骰子实现了简单的正态分布,保证收益最大化在中间数,低值低风险低收益,高值高风险高收益
3.5原型3总结
只说这个原型,还有一些优化的空间,例如:
1生存能力的资源获取随机,会造成节奏拖慢,我们可以把资源获取中的永久生存能力的随机获取去掉,更进一步,可以直接去掉临时生命力,只保留临时机动和临时攻击的设定。
2机动性补充公式需要优化,实际不是输出或生存掉一点,机动涨一点。经过验算后可以维持机动力设计,但需要尽量保证15点分配左右以及555均衡分配,则误差较小
最后,非常建议大家上手玩一下原型3,其中设计亲手游玩体会更深,原型3已经具备一定的可玩性,重玩性,涌现平衡优劣势,玩家对战局环境的影响和反馈也体现了一部分,同时,即使没有中央控制系统,该原型也体现了一部分对节奏的调控能力,还算比较优雅。
同时,让我们回忆一下复杂系统和涌现的目的,也是我们实现的目标:
- 产生有意义的变化,来提供新的体验
- 增强玩家对环境的影响与反馈
- 平衡优劣势,拉近不同水平玩家距离,降低操作和策略门槛
- 改变和控制节奏
- 承载不同类型玩家的游玩需求
- 部分替代其他玩家的作用
这个原型,在一定程度上,已经将前4条优势体现出来。然而,这还只是一个比较简单的原型,如果我们将资源视作一个单元,当前方案只有一种输入,单个玩家的输入。也只有一种输出,对单个玩家的输出。这是规则类涌现的一个典型,所以接下来,我们将尝试基于代理的涌现原型设计。
十二、原型4九宫格涌现
4.1设计目的
我们先假设单局战斗中存在一种第三方单位作为代理,这种单位需要实现复杂系统的6个目的,那他们如何最简单最直接的实现?如何由目的倒推对复杂系统的要求?具体分析如下:
1.产生有意义的变化,来提供新的体验
提供新的验证场景,将我们想要考验玩家的点放在这些单位上来实现。新的验证场景,例如如果要考验玩家的形状,或者其他单纯敌我单位战斗考验不到的东西,则要先考虑,是否可以放在敌方单位上面,若是不能放在敌方单位上再考虑放在复杂系统上。
反过来思考,什么是敌方单位不能实现的,就是应该由复杂系统来实现。例如敌方单位由对方玩家来决定,一些可控稳定的需求无法实现,系统由设计师来定,可以更可控。例如敌方单位会尽量偏向敌方优势,系统可以承载双方中立平等的设计。
2.增强玩家对环境的影响与反馈
作为反馈的一环,则是将对玩家做的任何行为尽量明确放大的反馈给玩家,并对战局有意义。反馈需要复杂系统对玩家的行为等信息敏感,并且需要做出符合玩家认知的反应
3.平衡优劣势,拉近不同水平玩家距离,降低操作和策略门槛
拉平玩家差距,这些单位会帮助弱势的一方,需要复杂系统可以识别出敌我双方的优劣势,并且做出反应
4.改变和控制节奏
代理需要在合适的时机,改变和控制节奏,例如残局时加快节奏等等
5.承载不同类型玩家的游玩需求
承载不同目的的玩家,根据目的设计,例如击杀AI单位局外获取更多金钱,可以击破擂台攻击观众等。
例如分化玩家的目标,局外塑造多种单局追求,局内才能体现。
例如除了战胜敌人之外,类似coc来搞资源是一种,为下一局做铺垫局与局之间做关联,给与弱势玩家一个补偿,但是更适合异步PVP。
例如单局之间的关联,可以是让代理有记忆能力,根据玩家过去做的行为,影响超越单局。
例如有NPC阵营,对玩家有好感度,在单局游戏中随机遇到,视对双方的好感度,对双方玩家做出不同的行为
于是玩家在游戏中可以有第三种目标,刷阵营好感度,或改变对方阵营好感度,或者阵营可以发布任务,完成任务作为第三种目标。
6.部分替代其他玩家的作用
复杂系统需要整体上给与玩家足够多变的挑战,代理需要和玩家拥有一致的底层规则。
上面是我们的目标,一步步来,接下来,我们将会引入最简单的代理,代理的行为也很简单,挑选一个合适的目标,进行战斗即可。同时我们需要用简单的规则,让多个代理在整体产生涌现行为。
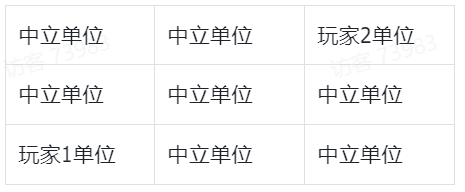
4.2玩法规则
战场为一个九宫格格子地图。除了双方玩家外,地图上有7个中立单位,开局时用10面骰子随机中立单位的攻击属性和生命属性,机动力固定0忽略,玩家单位和前述原型一致,自由分配15点属性。如下:
每个回合开始时,遍历九宫格所有中立单位,向所有附近非中立单位进攻
中立目标选择的逻辑是单元格总输出最高》生存最高》随机
进攻单位格有玩家单位时,该玩家可自行选择用雇佣单位还是本体来先防御
战斗规则和原型2基础战斗一致,中立单位和雇佣单位机动视作0
玩家行动阶段,机动性高的一方先行动,可以消耗一点机动性移动到附近格或不动
移动阶段完成后,所在单元格若是友方单位,无事发生,敌方单位或中立单位则战斗
若是中立单位则直接战斗,若有敌方单位则和敌方单位进行战斗,战斗规则一致
若既有敌方单位又有敌方雇佣单位,敌方可选择谁来迎战,战斗结束后,敌方下个回合可选择继续进攻
当玩家战胜所在格子的中立单位或敌方雇佣单位后,若该格子没有其他我方雇佣单位,可以选择消耗自身的属性,生成一个我方雇佣单位,雇佣单位属性为消耗属性的两倍,机动力固定为0
例如玩家攻击为5,生命为8,可以消耗N点攻击,M点生命,生成一个2N点攻击,2M点生命,0点机动的我方雇佣单位
当玩家行动完毕后,回合进入结束阶段,结束阶段若是地图上有空位,随机生成中立单位
4.3原型4总结
上面是最基础的代理模拟,其中用移动能力的消耗来防止滚雪球是合理的,并且原型4的中立单位已经对游戏产生一定有意义的影响,甚至可以“涌现”出最简单的夹击,可不要小瞧这个简单的夹击,它就类似康威生命游戏中的元胞自动机行为,都是由最简单的规则(原型中的中立单元选择目标规则),自行出现的一些现象。这个原型中的涌现也许简单到一眼看穿,但仍揭示了涌现的本质。
虽然原型4基本是成立的,但仍有以下的问题:
- 消耗机动性进行地图位移不合理,不是同一个层次的移动资源,额外需要设计一个大地图移动能力,和机动性相关,但是不同层次需要独立。
- 需要防止消极逃跑的策略,加入主基地?加入移动能力变化?加入大地图远程伤害手段?
- 高风险高收益需要更明确简洁的吸引力和反馈。
- 有地形后仍缺失创造局部以多打少的策略能力考验场景,以及少打少的维持能力,用于提供调度资源的空间和时机把控可能性。
十三、原型5主基地涌现
5.1设计目的
吸收原型4总结的优缺点,我们进一步进行优化的同时,将更多目光转移到,涌现如何参与进一个合理的目标挑战反馈结构。先复习一下什么是好的目标挑战反馈结构?一场战斗,是由多个并存,嵌套的大小目标,挑战和反馈组成:
1目标
- 合理,有难度但够得着的目标,可以被分解的目标
- 不同类型层次的目标,大目标永远有希望但难达成,作为最终追求hook
- 中目标有挑战但在能接受的延时反馈的极限内能达成,作为阶段反馈
- 小目标作为容易达成或容易失败后快速学习达成的填充反馈
2挑战
- 有了目标,就要设置挑战,挑战是一切的核心,也是最难的部分
- 对不同大小的目标,要有不同的挑战,好的挑战是需要有难度但能完成的挑战
- 最好的挑战就是使出浑身解数刚刚好极限完成的挑战,方法一般有自适应变化的挑战难度,自适应变化的目标,将失败作为挑战的一环,模糊挑战的概念等等
3反馈
- 和目标以及挑战不同,不管什么大小的目标和什么难度的挑战,反馈都有共同的要求
- 首先,反馈有标识进度的作用,使得玩家知道自己在这个挑战的什么阶段,离目标有多远
- 人类的感知是不均衡的,离终点远时,或未知终点距离时,会放大这个距离,离终点近时,会缩小这个距离。所以,及时,明确的分阶段反馈,能够帮助玩家更好的进行一个挑战,靠近一个目标
- 其次,正向的反馈,给与玩家动力,给与玩家操作的确认
- 最后,负向的反馈也很重要,教学玩家,惩罚玩家,反向激励玩家
之前我们已经说过涌现的优势,对于这个目标挑战反馈结构当然同样适用,我们来实际尝试一下:
5.2玩法规则
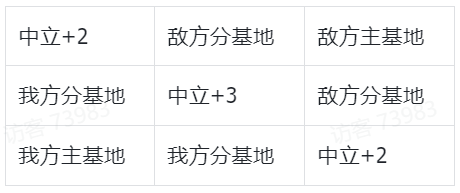
还是九宫格地图,每个玩家拥有一个主基地,主基地被占领则失败,地图设计如下:
分基地和原型4的雇佣单位一致,只不过是初始固定给与我方的单位
主基地属性可以为9攻9血,分基地可以为5攻5血,属性可以适当自己调整试试,会决定游戏节奏
玩家操控的单位或者主基地被破坏,则游戏失败
玩家操控的单位每回合可以移动一格
回合流程是机动力高的一方先移动
玩家操控单位所在的格子没有敌方和我方其他单位时,可以产生雇佣单位,产生规则和原型4规则一致
双方移动完后,所有建筑可以向相邻格子分配点数产生雇佣单位,每个格子友方非玩家操控单位数最多2个
双方轮流操作后,进行战斗环节,战斗环节规则不变
额外的,单个单位属性值不大于9
5.3原型5总结
相比原型4,原型5解决了一些问题,例如消极避战,机动资源不合理等。同时,对于目标挑战的优化,体现在结果上,我们会发现玩家的策略自由度会高很多,可以基于简单的九宫格进行一些更复杂的策略,例如创造局部以多打少等。同时,我们最关注的涌现部分,仍旧和原型4接近,没有什么损失,反而,因为玩家的决策自由度增加,在感知上,涌现部分会更加突出,这也是这个原型体现出的一个有趣的现象。由此我们可以知道,对于涌现的利用,至少需要一定程度的策略自由度,有了策略自由度,才能对整个复杂系统做更多输入的可能性。
下一步,我们反其道而行之,做做减法,用更抽象的方式来实现一样的博弈。
十四、原型6抽象分阶段战场
6.1设计目的
根据原型5的验证成果,我们还可以进一步抽象,来感受涌现:
可以专注于资源分配,降低移动和战场位置的相关因素,更加抽象
雇佣单位的机动性很关键,往带机动性,更接近僚机而不是建筑的方向验证,中立单位还是可以是建筑
直接分配点数,基地可以换一种形式存在,同时点数的存在也为下个原型打下基础
加入战斗中途加入单位的设计,分散决策
6.2玩法规则
战场由战场效果和战场收益,以及中立防守单位三者组成
战场效果设计目的是辅助决策,平衡优劣势,有以下三种:
- 考验,若投入的单位总点数大于XX,则临时加成XX
- 辅助,若投入的单位总点数小于XX,则临时加成XX
- 消耗,加强中立单位X点
战场效果第一回合不揭示,回合结束后才揭示
战场收益,玩家追求目标,且可控,开始时就揭示
- 每回合增加总自由点数上限X,X随机,且决定中立防御的点数配比
- 增强玩家本身,暂时不用
玩家游戏开始时15点分配到自身单位,还有自由点数X点
开始游戏时放入三个战场,将战场收益揭示,战场效果不揭示
玩家每回合可以双盲做两个操作,将自由点数分配到三个战场中的一个,成为雇佣单位,和之前原型不同的是,雇佣单位可以有机动性,和玩家单位基本一致
玩家将自身单位移动到某个战场或从战场移回基地,玩家单位去另一个战场需要移回基地,如下图:
回合结束时结算战斗,和之前规则一致
每个战场除玩家单位外最多一个雇佣单位,有一个雇佣单位时,基地无法派遣新的
回合开始时自由点数回满,并且每个战场若没有中立单位,则重新随机生成一个中立单位
中立单位生成规则为6面骰,投三次代表输出,生存和机动,投到生存0则不生成
6.3原型6总结
原型6的体验和前两个原型又有所不同,虽然更加简洁,但可玩性反而相对更高,这是因为将空间位置博弈更加抽象后,可以反而可以强化单个区域的效果,对涌现的表现加成更大,这也是这个原型给我们的启发之一:
代理和环境的存在都是涌现非常重要的一环,他们都是复杂系统的组件,是相辅相成的,或者可以直接视为一体。
而在玩原型6的时候,也发现了一些可以更优的部分,例如第一步改为依次揭示战场可以减轻决策成本,也体现了不可控部分降低决策成本这一点。例如玩家操控单位会有点被中立单位喧宾夺主,战场收益还可以更高一点等。最重要的是,整体决策数较少,每一步决策负担过高。
十五、原型7细分决策平衡优劣势
7.1设计目的
根据原型6的验证成果,除了优化细节,我们来尝试将决策拆分,降低每一步决策的信息不确定性和负担,但每一步决策之间互相关联,考验玩家思维步数深度,从精确策略转向模糊策略,这是原型7的重点之一。
另外一方面,我们再次将目光放到优劣势平衡这一点,探讨利用局外资源带入局内和涌现结合的方式:
对于一个常规的带局外的单局战斗为核心的游戏来说,单局战斗最终目标是为了获取胜利的快乐以及奖励,奖励是服务于局外的发展,最终为了更好的进行单局战斗。同时根据养成,经验,技巧等等因素,对于一个玩家来说,战中刚进入对局时有3种状态:1明显强于对方,2接近势均力敌,3明显弱于对方。
对于玩家来说,略强和略弱以及势均力敌的情况是最常见的情况,且是我们期望最多的情况(通过elo匹配等方式)
在这种情况下,期望玩家目标是获取胜利,胜利的奖励大于其他路径。
有所不同的是,这种情况下玩家可以有两种偏向,第一是放大优势和缩小劣势后进行战斗,第二是直接进行战斗分出胜负,偏弱的一方会倾向前者,偏强的一方会倾向后者。
对于明显强于对方的玩家,我们需要给与一个更难达成,奖励更高,且过程中会削弱玩家的路径,例如破坏敌方基地,毁灭敌方所有建筑,攻击第三方单位等等。
反之,对于弱于敌方的玩家,可以是帮助第三方单位防御,获取防御资源等。当然也需要一个合理的胜负条件,要考虑弱势方是否会主动承受伤害,消极比赛,投降,快速结束比赛。
也不能通过简单的战斗力来供系统决定优劣势,会促进压战力行为出现,和复杂系统的结合,我们需要玩家根据战场情况自己判断双方优劣势,做出不同的决策,来决定优劣势。
那局外资源又如何去达成平衡优劣势的目标呢?这边探讨一种适合和涌现结合的可能性:
我们将玩家在战中的目标分为两大类,胜利和获取资源,两者不冲突但有侧重;
玩家的实现这两个目标的时候,有两种抉择,第一,减少局外获得资源以获取局内更强的战力,第二牺牲局内战力获取更多局外资源;
其中是渐进的变化,如此,不管优劣势方,都可以走两条路,风险和收益并存且由玩家自己把控;
举个例子,例如我们设一场战斗胜利可以获得10分的战利品,失败保底有2分的战利品。局内存在复杂系统(例如一个第三方阵营),玩家可以与其进行不同的交互,进攻会获取更多局外战利品,也会损伤自身的战斗力,也可以做第二类交互,用局外战利品的消耗或者减少,来增强自身的战斗力。
如此,我们达成一个目标,理论上玩家最优解是战力刚刚胜过对方能够拿下胜利的前提下,尽可能多的用战力换局外资源,这样一来,玩家间会与复杂系统一起,进行非常动态的博弈,自适应地平衡优劣势。
因此,原型7将引入一个新的资源,用来模拟局外带入局内的,除战斗单位外的一种可支配资源。
7.2玩法规则
共有三片战场,连成直线,一端靠近玩家A,另一端靠近玩家B,如下
玩家自己的旗舰初始在主基地,旗舰取消机动性,初始分配点数为10点,但是旗舰血量乘10
玩家每回合可以从自己的自由点数中分配N点成为一个雇佣单位,可以0点,双盲,必须生成在主基地
回合下一步双盲决定旗舰前进后退还是不动三项操作
下一步,所有雇佣单位所在的格子若没有敌方或中立单位,则自动向敌方主基地移动一格
下一步战斗结算伤害,规则和之前的原型一致
每个回合结束时战场会生成中立单位
中立单位生成仍旧是投6面骰子两次,分别作为输出和生存能力,机动性视为0
每个回合生成战场收益,收益大小随机投掷10面骰
加入利息设计,每N点回合结束时加1点,降低预测敌方的难度,同时增加博弈空间
加入占领成功一次性奖励,促进玩家更加激进,例如占领单位+1+1,或者战利品自由分配占领单位还是收回
战利品分配在下轮怪物和收益生成之后,双方雇佣单位之前完成
每个战场最多可以投两个雇佣单位
7.3原型7总结
原型7体现了将策略拆密拆细,这种方式会更加契合涌现的设计,因为涌现本身需要一定步长的决策深度来拉差。不止是涌现,在做设计的时候,我们整体上都会偏向将精确策略模糊化,不仅仅为了涌现,而是更贴合人类做决策的本能。
尤其在即时制游戏中,一般将精确策略作为额外深度上限提供,考验玩家对游戏的掌握,信息收集,反应,记忆,快速决策等能力。操作上来说,偏向高频操作考验反应,收益代价都较小,低频操作考验策略,收益代价都较大。操作速度,操作精准度,操作策略深度三者为不可能三角。所以对于我们来说,相比精确策略更偏向模糊策略,并且重点是利用涌现令玩家产生模糊策略是精确策略的错觉,再利用机制放大模糊和精确策略的反馈。
同时,更偏模糊策略配合前文所说的动态平衡优劣势才能成立。(完全精确策略,则优势玩家最优解很明确,优于敌方的前提下,将所有战斗力换为局外资源,劣势玩家则什么也干不了)
十六、涌现设计总结
感谢耐心看到这里的朋友,上面我们设计了七个原型,一步步展示了复杂系统和涌现设计的一些要点,原型都我自己快速设计的,比较简陋,如果在玩的过程中,有更好的想法,随时修改原型即可,达成设计目的就行。借由上述的原型设计,我来总结一下涌现设计的一些经验:
1.规则尽量底层,抽象,通用
对于复杂系统,复杂度来自代理间,规则间的交互,不在于规则本身的复杂度。反而,对于设计来说,用越简约的规则实现设计目的,越优雅,并且也好调试,预测和利用涌现现象。多次迭代的输入输出,每次迭代都尽量简单易懂,规则清晰。举个例子,我们设计一个元素反应的复杂系统,不该是去设计木头遇到火就会燃烧,火遇到水就灭这样的规则,而是应该设计更底层通用的规则,例如温度系统,所有这些元素会改变周围的温度,温度超过燃点就燃烧,低于冰点就结冰。如此设计,所有的涉及温度变化这个单一度量可以描述的元素反应,都统一起来了,不仅简洁,后续拓展性也强。这就是一个例子,规则越底层,越抽象,越简洁,越通用,才是一个适合复杂系统的设计。
2.博弈空间,决策复杂度,学习成本,玩家掌控程度之间的平衡
信息不能太完备,否则决策门槛较高,也不能太缺失,否则策略意义太小。一般通过逐步释放的方式来达成信息密度的控制。同时,信息除了对决策的影响,往往还影响玩家对战局的可控程度,这一点往往和涌现紧密相连,特别需要注意一个现象:某个信息和高收益相关,逼着玩家不得不去深入涌现,带来巨大的决策成本。同理,信息,包括复杂系统内部的规则信息,也无需急匆匆教学玩家,在有复杂系统的游戏中,不需要追求玩家过多的掌控程度,探索复杂系统本身也可以作为乐趣之一,对复杂系统的熟悉程度也可以作为不同玩家间的拉差。
3.拆分降低每一步的决策成本,及时反馈,减少长考
如原型7所说,策略拆密拆细,这种方式会更加契合涌现的设计,因为涌现本身需要一定步长的决策深度来拉差。我们追求的是玩家尽量用模糊策略来应对复杂系统和涌现,但是通过涌现结果,UI暗示等等设计手段,让玩家感觉自己在做精确策略,获得高反馈。
4.注意涌现中滥用随机
不可控部分大多数时候是降低策略成本,因为不需纳入策略考量之中,控制随机,对抗随机,利用随机,也能带来相当大的乐趣。涌现也是类似,他们都是不可控的一种,那有朋友就可能会想了,涌现加上随机会如何?
我们举个简单例子,模拟人生中的小人,他们有自己的想法,但这时候我们让某些想法出现的规则随机。这时候,对于这些想法的涌现部分玩家会如何看?结论就是看不了,滥用随机,随机会侵蚀涌现的意义,最后,变成随机盖过涌现的乐趣,或者两者互相影响。
我们再细一点,如果把涌现和随机的结合分为前中后三类:
- 我们会发现,涌现前随机,对涌现影响不大,但意义也不大
- 涌现后随机,会破坏涌现的意义
- 涌现过程中掺杂随机,大大增加不可控程度,实际上也在破坏涌现
所以,同一个游戏中,随机部分和涌现部分最好是分离开来,且可以随机的结果和涌现相关,但不要掺杂两者,或者涌现的结果再随机一道
5.平衡优劣势
需要给劣势方优势的同时,尽量保持规则统一,不要过度依赖涌现本身的不可控来平衡优劣势,更好的是以一个自洽的规则让系统合理的平衡优劣势,最好的是让优势方自适应追求高风险高收益,来平衡优劣势。例如前文说的局外资源带入的方式。
6.利用提前认知降低理解学习成本
复杂系统一般都有比较高的理解学习成本,并且现实生活中有非常多已有的复杂系统,因此,多多利用现实生活的提前认知,来降低门槛。例如原创设计了某些规则,那也去生活中找一个最接近的复杂系统,包装一下靠过去。
7.代理与AI的异同
代理不等于AI,这是常见的一个误区,因为很多时候他们两个有重叠的部分,但从设计上讲,一定要注意,代理是一个以一定规则执行输入输出的组件,它完全不需要追求智能,复杂,灵活等等,如果这样去设计,就跑偏了。可以看出上面几个原型,都会将代理设计的非常简单,重点不是代理本身多复杂智能,重点是代理与代理直接的交互规则,在整体上能否产生我们想要的涌现。好的代理应该享受和玩家操控单位一致的底层逻辑,但是利用好代理所独有的优势。就类似AI的设计,拟真AI大多数不是最好体验的AI,最好的是利用AI可以作弊这一点,更大化发挥AI对玩家体验的作用。例如类似求生之路的导演系统,光环敌人AI等等达成的效果。
代理不等于AI,但是可以参考AI和玩家可以用的策略,来进行设计,以下是我对1V1对抗的策略博弈的一些不完整总结:
- 最简单石头剪刀布,离散的循环克制,最基础的策略
- 上校博弈,资源分配策略,以弱胜强,在总资源的基础上博弈资源分配能力
- 连续循环克制,例如某资源高一点优势,高太多反而是劣势,大多配合上校博弈或资源规划
- 竞价博弈,双方花费资源竞价一个目标,一种连续的心理博弈
- 加注博弈,典型的就是扑克单挑,同样是连续的心理博弈
- 深度博弈,比拼思考步长,大多数棋类
- 竞速博弈,双方比拼达成目标的速度,本身很难成立,一般辅以双方交互的设计,麻将就是典型,或者是和其他策略设计结合,比如结合上资源规划
大多数实际的策略,是由上面多种设计复合配合,而这些策略,都可以应用于代理的设计。
8.超越复杂系统
最后,本文探讨的是,复杂系统和涌现在游戏中的利用方法,我们追求的从来不是模拟一个复杂系统,或是多么追求和现实一致的涌现。我们追求的是利用复杂系统和涌现,服务于我们的设计目的。
所以我们要学习复杂系统,但要超越复杂系统,我们可以重构现实的复杂系统,例如流浪方舟里面实现的设计物理,就跟真实物理不同。同时,我们也可以有外力给与系统,不用追求完全的系统内部达成自适应,也可以主动放大涌现等等,当然,当复杂系统和涌现对核心玩法没有帮助时,不要犹豫,砍掉,一切为设计目的服务。
十七、结语:涌现,生命,智慧
上面8个章节,都是以一个设计师的视角,较为理性地去剖析复杂系统和涌现,目的性非常强地探寻其在游戏中的利用方式,希望对大家有所帮助。接下来最后一章,随便聊点不那么理性的感想,随便交流谈笑一番。
对复杂系统和涌现现象的着迷,离不开对自己对生命和智慧的敬畏与好奇。很多朋友不知道,生命到如今也没有一个准确的定义,生命是什么?和复杂系统如何定义类似,这是一个至今没有完全达成共识的话题,科学家们只能对生命提出了一些较为普遍的特征,例如:
- 结构,生物体的各种化学成分在体内不是随机堆砌在一起的,而是严整有序的结构。只有当大分子组成一定的结构,或形成细胞这样一个有序的系统,才能表现出生命现象。
- 新陈代谢,生命会与周围环境不断进行着物质交换和能量流动。一些物质被生物体吸收后,在其中发生一系列变化,成为最终产物而被排出体外,这被称作新陈代谢。
- 应激性,生物能接受外界刺激而发生反应。包括感受刺激和反应两个过程。
- 自我复制。
- 进化和适应,生命通过遗传和进化,可以适应不同环境。
以上只是一些特征,生命的定义多种多样,至今没有准确定义。而从复杂系统的角度来定义,生命不过一些简单的组件聚集在一起,所涌现出来的整体现象。就像美国物理学家默里·盖尔曼(Murray Gell-Mann)曾说:我们在周遭世界所见的复杂行为——甚至在生命世界中——只是“从深奥的简洁中浮现出的复杂表象”。
有人也会问,涌现是否只是一种错觉,是我们主观强加给系统表象的意义?这个问题,其实和智慧是否存在,是否是大脑的错觉没有本质的区别,每个人也许有不同的答案,但作为一个智慧的载体,我很难承认,我们仅凭错觉能够建立起我们璀璨的文明,留下名传千古的诗篇,但是也许在更高智慧的生命眼中,我们的文明火花,不过是蚂蚁抱团表现出来的蠢蠢集群智慧,说不得还被定义成集群效应,戴不上智慧的王冠。
而对游戏来说,前面几章没有深入探索的最后一部分,就是复杂系统部分替代其他玩家的作用这一点,正是来源于对涌现生命智慧三者关联的启发。这一部分来自我们最新对长线游戏的思考——对于一个着重创意设计的小团队,怎样的方向最适合做长线内容。这是一个很大很重的话题,这里不展开,以后有机会单独写文章,先直接说我认为的三个可行方向:
- 多人竞技,靠多人之间的交互博弈,不断产生新的内容。
- 利用涌现的代替玩家的部分功能后,1V1的竞技,弥补1V1竞技人人博弈产生内容不如多人的部分。
- 利用涌现或其他方式,高重玩性高设计空间的单局PVE,高效更新关卡来做长线。
以上是一家之言,只适合我们自己团队,仅供参考,其中第二点,就是我们一直在探索的方向,如何利用涌现模拟玩家,让系统能够代替部分玩家间互相给予的体验。就像之前说的,这里不是要做一个拟真AI去模拟人的智能,而是用涌现系统,去模拟人类玩家给其他玩家带来的那种,
理智中带着混沌,可控中混杂着不可控,冲动疯狂和理性决策交缠的感觉。
好吧,写着写着又想着对游戏设计的作用,职业病发作,本篇文章前后耗时数月,可能有些啰嗦不连贯,感谢耐心看到这里的朋友,欢迎多多交流,也欢迎关注我的公众号《鱼塘游戏制作工坊》。
下面就用一段上篇文章被我删掉的胡言乱语,来结束这篇文章吧!
“生命与智慧不是偶然,而是必然。
热力学第二定律-熵增定律表明,一个封闭系统,整体混乱度会随着时间流逝增加,直到所有事物都走到最无序的状态。于是维多利亚时代的热力学家想象,宇宙这个封闭系统,所有能量也会慢慢转化成废热,恒星各自熄灭,黑洞也会耗尽自身,最终所有一切都会处于平淡一致的寂灭,这就是所谓的“热寂”。然而,在这个不可逆的过程中,宇宙似乎有些不甘,逐渐平静下来宇宙海洋,在某些角落骤起波澜,一些有序的构造体,从无序的物质中涌现出规则。这些构造体在行星的原初羊水中翻滚,用尽全力吸收恒星的光芒,用简单的碳元素做骨架,配上一些别的东西,堆积出复杂的自适应系统,有些甚至还能开出漂亮的花朵。虽然,这些微小秩序的产生需要来自系统之外的能量,代价是宇宙其他区域更多的混乱。
可是,宇宙在走向无序混沌的过程中,还是在一些角落悄悄孕育了有序的生命,它们是如此的珍贵,那是宇宙对抗无序的呓语,是宇宙为自身加冕的桂冠。而生命中涌现出来的智慧,更仿佛是宇宙的呓语恰好吟唱成了一曲歌谣,是桂冠上璀璨的宝石,是奇迹中的奇迹。每个人的心灵,都是独一无二,从混沌中挣扎着长出的花朵,每个人的灵魂,都是宇宙灵魂的一部分。
所以,用力活着,用力地思考,不辜负这奇迹。”
感谢您的阅读。
作者:余田,《流浪方舟》制作人,微信号yutianTerean
欢迎关注作者个人公众号“鱼塘游戏制作工坊”