一个神秘且不可思议的事实是,我们的宇宙遵循的自然律最终总能用微积分的语言和微分方程的形式表达出来
——《微积分的力量》
游戏数学建模的实际工作大约分为两块,一块是依据系统规则投放战斗属性与经济产出的具体值,另一块是设定成长或游玩节奏,即玩家如何随时间获取这些战斗属性与经济产出。前者是个简单问题,本文不关心,后者可以用微分方程建模。
比喻性的说,游戏的整个数据如同我们做了一大块蛋糕,蛋糕本身提供激励与快感(战斗属性与经济产出的具体值、游戏巧妙的玩法设计与剧情),同时我们会因玩家吃下蛋糕而给予奖励(消耗掉经济产出获得战斗成长或外观颜值)。我们不能让蛋糕太快被吃完,因此需控制玩家在时间轴上如何吃这块蛋糕,这次吃多少下次又吃多少(设定成长与游玩节奏)。显然这就是微分方程可以刻画的:
dy=f(y,t) dt
也就是说某时间点吃掉的蛋糕是这整块蛋糕的一个变化值。我决定在之后使用蛋糕的比喻,这可以省下因为不统一而冗长的数值用语。此外,本文沿袭《游戏数学建模工程手册》里的风格,尽可能使用工程数学的阐述方式,从而免去那些无谓的非专业争论。
首先我们必须对游戏系统做一些定性理解,然后试着用定量模型描述它们。玩家初始接触游戏并不能得到蛋糕被吃下给予的奖励,即:
y^' (t=0)=0
y(t=0)=0
这称微分方程的初始条件。对于战斗属性,角色不可能初始为0,它属于微分方程一个解的常数C>0。接着,游戏内容在绝大多数情况下是有限的,比如角色最高级打最高级的怪,这个怪的掉落是恒定的,因此在每天的24小时里击杀怪物产生的掉落是一个恒定值;再如主线关卡只设计了20章节,玩的足够久的玩家再怎么打也只能每天重复获得20章节的产出,于是:
y^' (t→∞)=M
换言之,游玩时间足够长,由于游戏内容设计的有限性每日产出是一个常数M,这称微分方程的边界条件。我们需要一个微分方程模型,能够容纳这2个描述了游戏系统规律的条件。我给出的模型是:
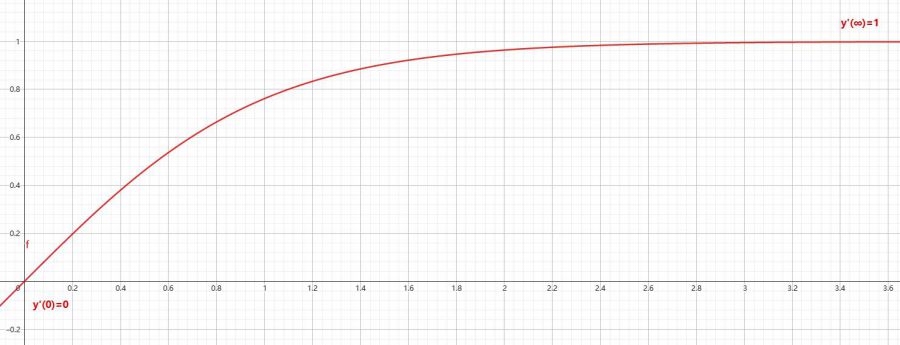
dy/dt=a⋅tanh(b⋅t)
即假设蛋糕每天被吃的情况与双曲正切函数成正比,双曲正切有如下图像:
其中a和b是待解参数,t为时间,t=0时为0,t趋于无穷大时=1,整个方程趋于参数a。这意味着a和b不是2个单纯的参数而是具备了现实意义,参数a表示一个游戏系统设计内容有限,b控制t的最终值表示该系统的损耗速率,b越大越快趋近于a,将更快到达该游戏系统的有限内容。另一种建模方案是:
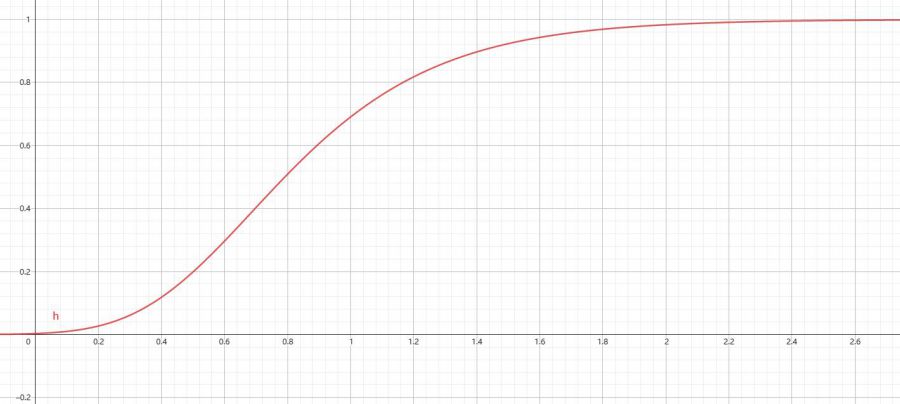
dy/dt=a⋅(1+e^(-b⋅t) )^(-α), α>0
这是广义logistic模型,一个恰当的α值在0点附近让蛋糕每天被吃的情况是缓慢增加而非双曲正切那样近乎线性增加。这个微分方程无法用初等函数写出解析解,拟合参数a、b、α需用差分法逼近导数值,计算时要在excel里手写龙格库塔算法,因此简便起见先于双曲正切模型下讨论。
我们得到如下解析解:
y(t)=a/b⋅ln[cosh(b⋅t)] +C
若计算的是角色的战斗属性成长,则C等于角色初始属性,对于本文讨论的经济建模而言不需要C,但是C如果有赋值,说明是一个开局就因付费或其他原因得到些许蛋糕的玩家,如WOW里的传家宝、老玩家邀请新玩家给予新玩家的奖励。y、y的一阶导和t我们是知道的,用以拟合出未知参数a与b,准确的说是我们去规划玩家每天吃掉蛋糕的具体量。以下是一个实际例子:
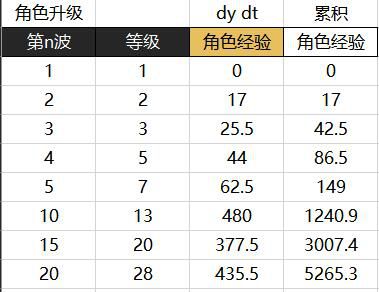
这个游戏系统的规则是每波战斗有不同类型与数量的怪物,每个怪物被击杀令角色获得升级经验、金币或其他经济道具,不同类型的怪物有着不同的经济产出值。图里仅考察前20波,领导或我们是不可能细腻规划这个角色的1级至28级具体在哪一波(如果这个系统要玩365天,角色有100级,这只会累死)。因此实际工作中只能规划关键节点,即图里的第1、2、10、15波期望的角色等级是多少。图中第1列是面对第n波怪,即战斗尚未开始,前波战斗已结束,第3列是统计前一波被击杀的怪物合起来的产出值,即y的一阶导具体值,第4列是前n波被击杀怪物合起来的产出值,即y的一个具体值。将该设定以{0, 0},{1, 17}…{4, 149},{19, 5265.3}的矩阵形式输入给matlab、mathematica等数学软件,拟合解析解表达式可求出a=0.83104,b=0.038109。现在,我们比对微分方程建模到底比其他方法有多好:
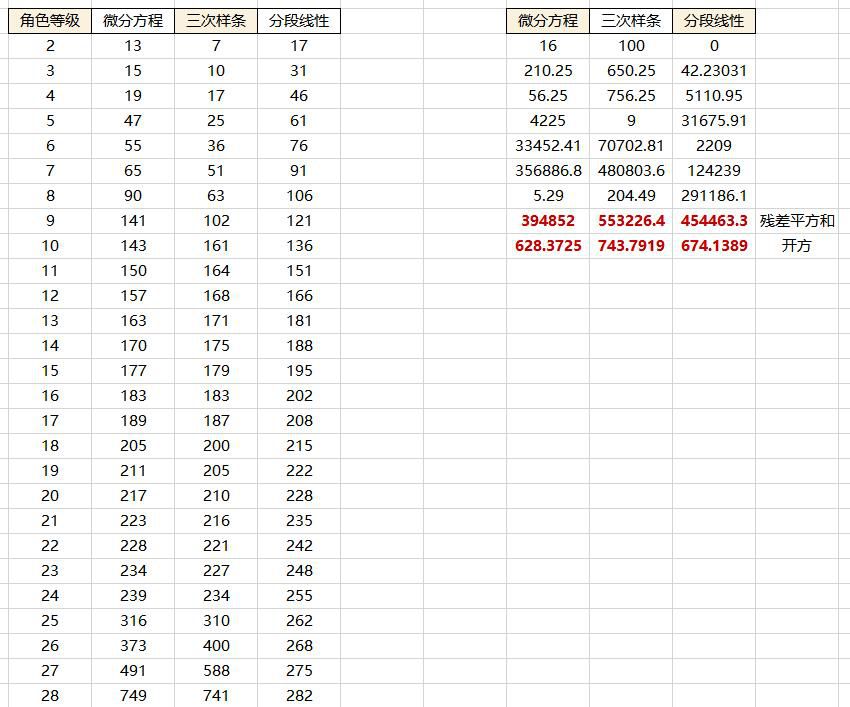
上图左边区域表示升到这个等级需要的经验值,分别是微分方程、三次样条插值和分段线性插值的估计结果,三次样条插值是用分段三次多项式逼近蛋糕随时间被吃掉的情况,分段线性插值是大多数数值策划会很自然想到的方法。右边区域使用残差平方和衡量模型的好坏,具体计算是用3个模型得到的累积值与关键节点的累积值相减后平方。可以看到微分方程模型与我们想要的节奏规划误差最小,其次分段线性,最后是三次样条。然而分段线性计算具体等级需要多少经验的结果是极其诡异的,实际工作中还要对结果各种修修补补。从理论分析角度,分段线性插值是一个步长很大的欧拉数值积分,而欧拉法在数值解微分方程时是精度最差的,误差随步长扩大加剧,因此分段线性是一个很差的模型,三次样条相对好些,可以看到图中左边区域与微分方程的每个结果接近程度较高。
注意参数a的值,前面的建模分析里我们可以知道a应当拟合出恰好是这个游戏系统在t趋于∞时的值才对,为什么是一个小于1的数?原因在于我们的游戏系统不管是战斗还是经济数量级往往较大,可在前期时数量级又特别小,则b必须是一个特别小的值才可能和a相乘后得到数量级小的值,一个特别小的值对于计算机是不友好的,截断误差会不可避免的累积造成错误结果,这影响了计算稳定性,需将关键节点矩阵的值适度缩小再求拟合,使用时乘回缩小系数即可。
现在,让我们仔细考察吃蛋糕的微分方程建模。注意看,我们的领导要求第4波能够从3级升到5级,然而关卡策划投放的怪物满打满算下来才提供44点角色经验,怎么可能分给4级和5级,却仍比3级的25.5高呢?我们应该让关卡策划增减这个地方的怪物数量、类型吗?显然不合实际。我们应该去修改这个关卡的具体怪物给多少角色经验、金币和其他经济道具吗?同样不合实际,因为那些怪物不是只有本关才用到,在前面的波次、后面的一些波次可能有被用到。即只要某日的产出与前面几日的产出“共享”一部分产出源头,就意味着吃蛋糕的规划细节,不管是谁来规划,都暗含了主观、一厢情愿,这种一厢情愿体现在与客观的怪物数量、产出规则有矛盾。于是,我们使用的建模方法,其实质意义在于折中、妥协,用更合理的模型去尽可能接近吃蛋糕的规划细节,真实的吃蛋糕规划必然存在一些节点是“异常值”,规划的节点越多“异常值”就越多,这也是为什么密集规划主要在前期,结果前期更容易出现不合理的原因。换言之,那些规划节点不总是合乎逻辑、符合客观的,不能随便去强行往上靠,使误差为0,使战斗与经济完全服从这些规划。微分方程的计算结果自动地、尽可能多地修正了这些异常,但又尽可能贴近实际想要的(残差平方和最小),微分方程的建模思路让我们更深刻认识了吃蛋糕的规划与蛋糕本身之间的关系。
巴比伦派数值策划:813299364