多智能体强化学习及其在游戏AI上的应用与展望

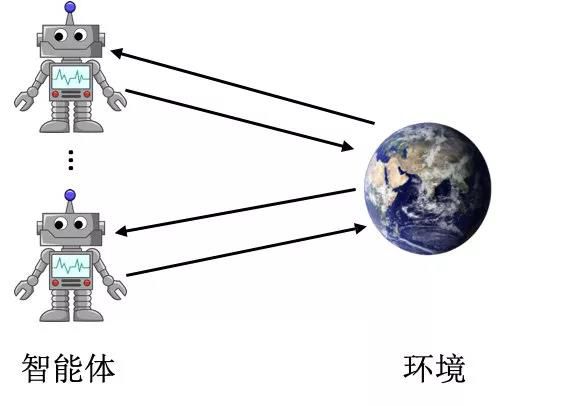
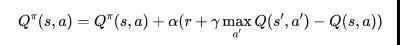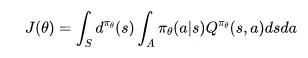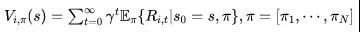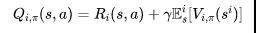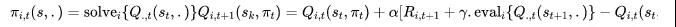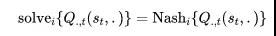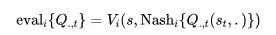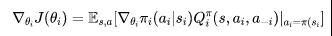近年来，人工智能技术在很多领域都取得了亮眼成就，并逐步从感知智能向决策智能迈进。强化学习是实现决策智能的重要路径，而现实世界中往往存在着多智能体的交互，也催生了多智能体强化学习的发展。这篇文章主要对多智能体强化学习进行整体阐述，并对其在游戏AI上的应用进行探讨与展望。

一.引言

近些年来，随着机器学习算法的持续优化和创新，计算资源和分布式计算系统带来的算力提升，以及可利用数据量的大大增加，AI(人工智能)技术迎来迅猛发展，在众多领域取得亮眼成就。

在图像分类、目标分割和目标检测领域最常提及的ImageNet计算机识别挑战赛中，取得 SOTA 的模型参数量的逐年增加(AlexNet参数量60M，FixResNeXt-101 32×48d参数量829M)，其在各项任务中取得的效果也越来越好。这一系列成就促进了利用人脸识别技术来验证身份，解锁手机，抓捕犯罪嫌疑人等方面的多种落地应用1。语音识别上，在很多细分场景中也取得很多瞩目成就，国内的三家公司搜狗(Sogou)、百度(Baidu)和科大讯飞(Iflytek)均在2016年召开发布会宣布各自的中文语音识别率准确率可达到97%以上2。目前在多语言间的翻译，语音转文字等方面都极大地方便人类的生活。信息流和商品的推荐上，人工智能技术帮助人们在浩如烟海的信息中快速的匹配到自己感兴趣的内容和商品。

另外，一些生成式的技术也获得广泛关注。对抗生成网络(Generative Adversarial Networks，简称GANs)是一种通过对抗过程生成模型的AI处理框架3，基于GANs处理框架，可以从无到有生成新的内容，比如英伟达(Nvidia)在2018年发布了超逼真的人脸生成AI系统4，可以按照某种要求生成细节极其丰富的人脸图像。Facebook AI团队最新出品的“文字风格刷”（TextStyleBrush），它只需要一张笔迹的照片，就能完美还原出一整套文本字迹来5。


AlphaGo在围棋项目上的卓越表现在学术界和工业界引起了深度强化学习的一股热潮6。2016年3月，AlphaGo战胜韩国围棋高手李世石，2017年5月，在中国乌镇围棋峰会上，AlphaGo Master与排名世界第一的世界围棋冠军柯洁对战，以3比0的总比分获胜。10月机器狗对狗大战，最强的新版AlphaGo Zero以89：11的战绩打败了曾经战胜柯洁的旧版AlphaGo Master。之后，深度强化学习技术一路高歌，OpenAI在Dota2上开发的OpenAI Five可以达到人类顶尖水平7，Deepmind在StartCraft上开发的AlphaStar也达到了人类职业玩家的水平8。

整体上看，AI的能力在之前的固定环境下的“听、说、看”等感知智能领域已经部分达到或超越了人类水准，后续将持续地向决策智能演进，即AI不仅需要知道环境是什么样的(会看，会听等)，还需要知道在具体的环境下做出正确的决策，才能在真实世界中发挥出更大价值。除此之外，之前的很多研究都是隐含假设了只有一个智能体(single agent)，而把其他部分当做环境的一部分进行处理。然而，实际环境中往往要考虑和其他个体交互，存在诸如合作，竞争等情形，比如机器人装配/足球，自动驾驶中的多车辆避让，以及游戏中存在的各种复杂的场景设置。


从算法技术层面来说，近年来感知智能上的重大突破很多是由于深度学习技术强大的表示学习的能力所带来，而决策智能的发展则需要依靠强化学习的范式来往前推进。同时，由于现实世界中多个智能体之间交互关系的存在，在强化学习的基础上，又进一步地引入了博弈论的知识，并发展出多智能体强化学习这一领域，以解决更复杂的现实世界中的决策问题。

当前，多智能体强化学习已经有了一定的发展，取得不错成绩。这篇文章主要就是详细梳理和介绍其整体脉络和发展情况，并对其在游戏AI领域中的应用进行探讨和展望。


二. 博弈论基础

01：引言

博弈论的发展具有一定的历史,  时至今日，已有18位博弈论的专家获得诺贝尔经济学家，展示了博弈论的影响力和重要性。

早在1934年，Stackelberg就已提出了斯塔克尔伯格均衡(Stackelberg Equilibrium )的概念；而更广为所知的纳什均衡(Nash Equilibrium )的概念也在1951年由Nash提出。1951年，Brown提出了重复博弈中的虚拟博弈(Fictitious Play)的概念来求均衡解；1965年，Selten提出了扩展式博弈中的子博弈完美均衡；1967年，Harsanyi则针对贝叶斯博弈提出了贝叶斯纳什均衡；1973年，Smith & Price进一步提出了演化博弈论；Aumann提出了Correlated Equilibrium；1994年，Papadimitriou则研究了均衡计算的复杂度，提出了PPAD的概念9 10。

博弈论发展过程中，有各个领域的科学家和研究人员参与，涉及的领域有经济学，数学，计算机科学等等。各个领域的人所关注的重点存在很大不同，经济学家更侧重于观察和提出一些均衡的概念来对真实世界的现象进行描述，而不关心如何去计算或学习均衡解，而计算机领域的研究人员则更关注如何去得到均衡解，以及求解的复杂度等等。这里主要从几个角度上进行简要介绍，包括博弈论的基本概念，典型的博弈的形式，博弈中的策略的类型，经典的均衡概念，更进一步地，介绍我们所关心的学习问题。

02：博弈的组成元素

一般来说，博弈中存在三种必要的元素，其与强化学习中经常使用的术语有一定的关联。

第一个必需的要素是玩家(Player)，Players N=1,2，…，n , 其表示的是参与博弈的各方, 比如两个人的剪刀石头布的博弈中的两个玩家，可以看出，这与强化学习中所使用的智能体(Agent)的概念存在相似之处。第二个所必需的要素是策略(Strategy)，其表示的是参与博弈的玩家们所采取的动作，即整体策略空间，是所有玩家策略空间的笛卡尔积，A=A1×A2×?An，比如上述的双人的剪刀石头布博弈中，有A1={剪刀，石头，布}，A2={剪刀，石头，布},显然其与强化学习中所定义的动作有非常大的相似之处。第三个必需的要素是收益(Payoff)函数或效用(utility)函数, 表示的是博弈中玩家采取了某个策略之后所得到的回报情况u=(u1.u2,?,un),ui:A→R。

在一般的博弈建模中，都会有所谓的理性人假设，博弈中的每一个玩家都尽力以自己的最小经济代价去获得自己的最大回报。为什么需要这个假设的原因也是显然的，参与博弈的玩家可以选择合法范围内的任意策略，如果不加以限制，那整个博弈的计算过程将无法进行。当然，这样的假设在现实世界中也存在着明显的局限性和过于理想化等问题，这里就不过多讨论。

03：不同的博弈形式

1）正则式博弈和扩展式博弈

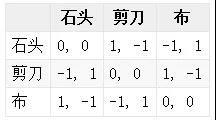
正则式博弈(Normal-form Game)，或者叫标准式博弈，指的是可以用矩阵或者表格的方式定义出来的博弈，即定义出上述的博弈三要素。比如上面的双人剪刀石头布博弈，就是一个正则式博弈，其中行表示的是一个玩家(row player), 列表示的是另一个玩家(column player)。表格里面的数值分别表示两个玩家在此策略下所获得的回报，比如石头对石头时，双方回报均为0，石头对剪刀时，列玩家的回报为1，行玩家的回报为-1，其他的可以依此类推。


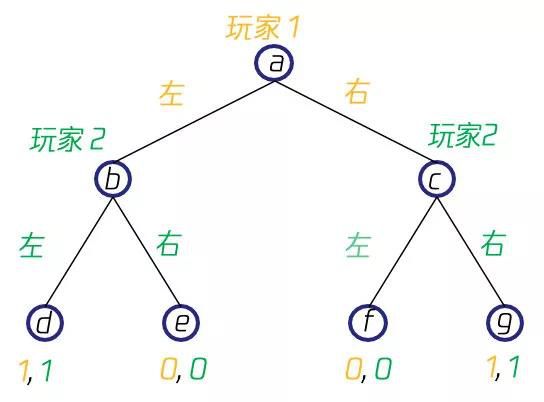
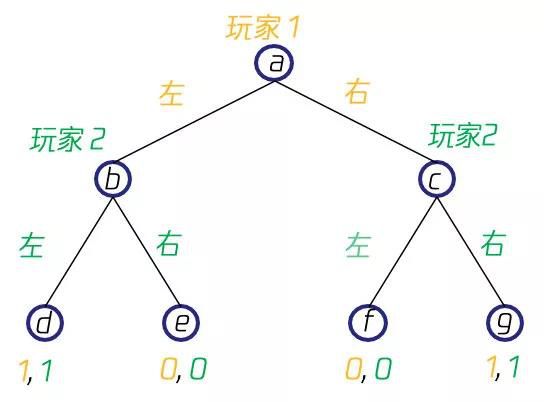
与正则式博弈不同，扩展式博弈(Extensive-form Game）不能用上述表格形式来描述博弈的元素，玩家在执行策略时存在着先后关系，需要用博弈树（Game Tree ）来进行表示。在博弈树中，非叶节点表示的是一个玩家的决策点，边则表示这个玩家所采取的策略，而叶节点则表示的是获得的回报。比如在一个简单的双人博弈中，双方依次做出向左或者向右的决策，当两次决策相同时，两人均获得1的回报，否则两人均获得0回报，则其博弈树会是如下所示的形式，起点a时玩家1采取了左动作到达b点，然后玩家2采取了左动作，到达叶节点d，此时双方均获得了1回报，其他情形也依此类推。


理论上说，扩展式博弈也可以用正则式博弈来表示，即转化为正则式的表达形式。采取的方式是将扩展式博弈中每一步可能出现的情形全部展开放在正则式博弈中，即将多步动态的信息转换为单步静态的信息表示。以上面的扩展式博弈为例，第一个玩家的可能策略有左，右两种，第二个玩家的可能策略有(左，左)，(左, 右)，(右, 左)，(右, 右)四种。其中，元组的第一个表示的是当第一个玩家采取第一个动作(左)时，第二个玩家采取的动作。元组的第二个则表示的是当第一个玩家采取第二个动作(右)时，第二个玩家采取的动作。当动作个数，玩家个数，轮数增加时，这个过程就继续增加。

从上面的例子中能够看出，虽然理论上扩展式博弈可以转换为正则式博弈，但是策略空间会随着参与博弈的玩家个数而指数变化，如上述简单例子中的第二个玩家22=4种动作。因此实际上在这样的场景中还是会按照扩展式博弈的形式来进行建模和分析，比如针对很多棋牌类游戏的建模。

2） 随机博弈

随机博弈是上述概念的进一步扩展，也被称之为马尔可夫博弈。与正则式博弈相比，其具有博弈各方同时执行动作的特性，并且，会继续执行多步。与扩展式博弈相比，其一方面是多步的博弈，另一方面具有了状态(state)的概念，与马尔科夫决策过程有相似之处。

具体地，其形式化定义可以被描述为(S,A1,2,?,n,R1,2,?,n,T，γ)，其中，S表示状态空间，A表示联合动作空间A1×A2?An, Ri=Ri(s,ai,a?i)表示的是第i个智能体的奖赏函数，T:S×A×S→[0,1]表示的是联合动作下的状态转移函数。同时，其具有了Behavioral Strategy的概念，以策略π:S×Ai→[0,1]表示，指的是第个智能体在当前状态下所实际执行的动作的概率，其与状态相关。


04：非完美信息与非完全信息

1）非完美信息

在上述过程中，均假设所有的信息对所有玩家可见，在很多博弈场景中并不适用。比如在一些MOBA游戏中，迷雾的存在使得对方玩家采取的动作并不都对我们玩家可见，同样地，一些棋牌类游戏中也同样存在类似现象。

存在一定的历史动作对一些玩家不可见的博弈，称之为非完美信息博弈(Imperfect Information Game)。在非完美信息的设定下，会存在一些状态我们无法区分(因为并不知道是之前做了哪个动作)，我们把这些无法区分开的状态集合称之为信息集(Information  Set)。比如上面扩展式博弈的例子，如果玩家1开始执行的动作对玩家2不可见，则{b, c}就是对于玩家2的一个信息集。


2） 非完全信息

前面所阐述的内容中，均假设了每一个玩家对博弈中的元素，包括参与博弈的玩家个数，所有玩家采取的动作(除了非完美信息)，玩家采取动作后的回报情况完全清楚，即知道全部的知识。非完全信息指的是玩家并不完全知道这些信息，对于执行动作所带来的回报并不完全清楚。一般来说，可以用博弈开始时，玩家是否有私有信息来判断是否为非完全信息博弈。比如拍卖，各个玩家对于商品的预期价格，可接受最高价格等信息就是博弈开始前玩家私有信息，比如麻将的初始牌也是博弈开始前玩家所私有的信息，因此这两个博弈均属于非完全信息博弈。

实际上，非完全信息也可以转换为非完美信息来进行处理，其主要通过海萨尼转换(Harsanyi Transformation)来完成。具体地，通过引入自然玩家(nature player)来参与博弈，但是只在博弈开始前发挥作用，完成其他正常玩家博弈前的准备。通过这样的方式，然玩家的历史动作对于正常玩家不可见，转换成了非完美信息15。

05：博弈的均衡

1) 博弈求解的基本概念

在博弈中，我们用ai,a?i分别表示第i个玩家以及除了第i个玩家外的其他玩家的动作。对于给定的a?i∈Ai×A2×?An,  称ai是a?i的最佳应对(Best Response, BR)?ui(ai,a?i)≥ui(a′i，a?i),?a′i∈Ai。也就是说，最佳应对使得就是在其他玩家采取时能够获得最大效用的动作。

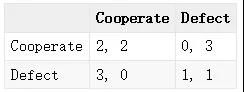
最佳应对是当其他玩家选择固定动作a?i时，第i个玩家所采取的“最好”策略，那么如果无论其他玩家采取何种动作，当前玩家ai的都是最佳应对呢？显然这个策略具有不论其他玩家如何决策，都存在优势的特性，也因此被称之为占优策略(Dominant Strategy，DS)，即， ai是占优策略?给定任意a?i，ai是最佳应对。比如在下图的囚徒困境博弈的例子中，考察列玩家， 由于3>2, 则Defect是其针对Cooperate的最佳应对，同样地，1>0, Defect又是其针对Defect的最佳应对，因此，在这个博弈中，Defect是列玩家的一个占优策略。


2）纳什均衡

纳什均衡应该是博弈论中最广为人知的概念之一了16。就像名字中所暗含的，其主要表达的是当前博弈环境中所能达到的均衡和稳定的状态，具体含义是，对于每一个玩家来说，当其他玩家不改变策略时，当前所有玩家的策略都是最佳应对，则称当前的联合策略达到了纳什均衡。这种情形下，任意一个玩家，都没办法通过只改变自己的策略，来获得更高的回报。形式化表达为: 一个联合策略a∈A是一个纳什均衡?对于任意玩家i来说，ai都是针对a?i的最佳应对。

比如在下面的Battle of Sex博弈中，双方都选择Party或都选择Home均为纳什均衡解，在这两处时，每一个人都无法通过改变自己的决策来获得更高的回报。而在下面的囚徒困境博弈中，虽然当两个人都选择Cooperate时，双方都可以获得2的回报，但是由于此时一方可以通过改变自己的决策来获得更大的回报，因此不是一个纳什均衡。只有当双方都选择Defect时，任意一方才都无法通过改变自身行为提高回报，达到了纳什均衡。从这个例子中，我们也可以看出，纳什均衡并不一定与我们直觉上的“最优”完全相同，其表征的是均衡的概念。


06：博弈的求解

在有了博弈的概念，均衡的概念之后，需要解决的问题就是如何去求解。目前博弈论领域有着众多的求解方法，我们今天主要介绍其中的几个。

1) Fictitious Play

Fictitious Play的概念Brown 1951年就已提出，其想法也很自然。博弈中的每一个玩家都维持一个关于其对手历史动作的belief，然后学习对这个经验分布的最佳应对。

如下面的Matching Pennies博弈，双方的博弈序列如表中所列，后面的beliefs是两个玩家分别出两个动作的统计值，会根据历史动作进行更新。这种方式虽然简单，但是其被证明在双人零和博弈，潜在博弈中均可以收敛到纳什均衡。


2) Double Oracle

Fictitious Play算法是保持对手玩家的历史动作的belief信息，并采取最佳应对。Double Oracle算法则是首先针对对手玩家历史上所有的策略求纳什均衡，再对这个纳什均衡采取最佳应对，如果这个最佳应对已在策略池中，则算法停止，否则将此最佳应对加入到策略池，继续下一轮，如此反复。这里的最佳应对被认为是“Oracle”(神谕)给出的, 且双方玩家均采取这种方式来更新策略，这也是Double Oracle这个算法名称的由来。

以剪刀石头布为例，如果采用Double Oracle来求解，其过程如下：

第0轮：

开始博弈，双方均只有石头，restricted game 石头 vs 石头

第1轮：

求解纳什：(1, 0, 0), (1, 0, 0)

Br1,Br2= 布， 布

第2轮：

求解纳什：(0, 1, 0), (0, 1, 0)

Br1,Br2= 剪刀， 剪刀

第3轮：

求解纳什: (1/3, 1/3, 1/3), (1/3, 1/3, 1/3)

第4轮：

找不到新的最佳应对，结束

输出(1/3, 1/3, 1/3)


3) No-regret Learning

Regret一般被称为后悔值或遗憾值。我们用at表示第t轮的联合动作，则玩家i在第t轮没有执行a′i动作的regret被定义为:Rt(a′i)=ui(a′i?at?i)。即执行a′i,能带来回报的增益多少，就是我们有多后悔没有执行这个动作的程度。更进一步地，从第1轮到第T轮到累积regret值被定义为:CRT(a′i)=∑Tt=1Rt(a′i), 即前T轮如果都做a′i能带来的总体增益。

在得到了regret以后，我们就可以利用其来决定动作的执行了，这就得到了Regret Matching方法，其含义是，在第t轮选择动作时，选择regret为正的动作(即有更大收益的)，并且选择的比例正比于regret(即收益更大的会更有几率被选择到)，当然，如果没有一个动作有正的regret，则随机选择一个即可。一个具体的形式可能是:图片。其被证明可以收敛到correlated均衡。

三. 多智能体强化学习算法基础

01：强化学习基础概念

机器学习研究的是如何通过数据或者以往的经验来提高计算机算法的性能指标，使系统能够在下一次完成同样或者类似的任务时更加高效。根据反馈信号的不同，通常可以将机器学习分为监督学习，半监督学习，无监督学习和强化学习。其中，强化学习的训练没有现成的样本，而是智能体在与环境的交互中收集相应的(状态，动作，奖赏)的样本进行试错学习，从而不断地改善自身策略来获取最大的累积奖赏11 12。


强化学习通常采用马尔科夫决策过程(Markov Decision Process, MDP) 来作为数学模型。一个MDP通常可形式化为一个五元组(S,A,T,R,γ),其中S表示的是状态的集合，A表示的是动作集合，T表示是在当前状态下执行某动作转移到某个状态的概率，R则表示对应的奖赏，γ表示折损系数。通常我们使用π(s×a)→[0,1]表示在状态s 下执行动作a 时的概率, 称之为策略(policy)。强化学习的目标就是去找到一个策略能使得累积奖赏最大:图片 。有两类主要的方法去求解，分别称之为基于值函数的(value-based)方法与基于策略的(policy-based)方法。

第一类方法主要是通过学习值函数来得到当前应当选择的最优策略，其常用的迭代方式是


第二类方法则是通过参数化策略的方式来直接学习π，即


其中dπθ是一个平稳分布。

02：多智能体强化学习

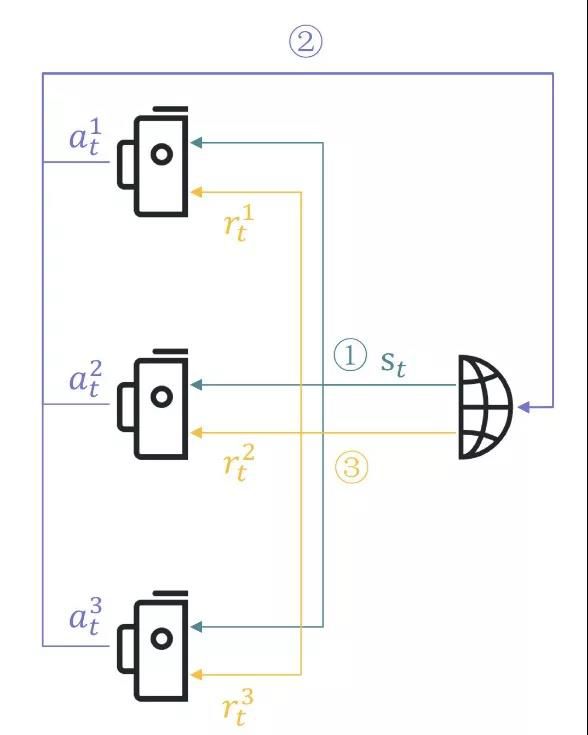
在传统的强化学习基础上，进一步引入多智能体的概念，就有了多智能体强化学习这一领域11 12。普遍意义上，多智能体强化学习采用随机博弈进行建模，有(S,A1,2,?,n,R1,2,?,n,T，γ)的表示，其中，S表示状态空间，A表示联合动作空间A1×A2?An, Ri=Ri(s,ai,a?i)表示的是第i个智能体的奖赏函数，T:S×A×S→[0,1]表示的是联合动作下的状态转移函数。


上述建模中，当n=1时，就退化为单智能体MDP，当状态空间|S|=1时，就退化为正则式博弈。另外，如果在上述要素上做出一些限制，比如，假设状态不是完全可见(非完美信息)，且所有的智能体的奖赏函数均相同，则其会变成Dec-POMDP，这也是目前合作类型的多智能体强化学习最常使用的建模方式。

按照这样的建模方式，同样可以得到类似单智能体中的值函数(value function)和状态-动作值函数(Q value function), 其具体形式如下所示，其中i表示计算第个智能体的情况，而是所有智能体的联合动作，合并发挥作用。

同样地，求解多智能体强化学习问题也有value-based方法和policy-based两类方法。然而，在多智能体的环境中，“最优”的概念会发生变化。比如对于完全合作的博弈问题，所有的智能体拥有相同的奖赏函数。而对于完全竞争的博弈，即零和博弈，一个智能体的目标是让其他所有智能体的回报最小，自己的回报最大。为了区分不同场景下不同博弈目标的最优，经典的多智能体强化学习的研究中用不同的均衡解概念，包括Stackelberg equilibrium，minimal regret，correlated equilibrium以及我们熟知的Nash equilibrium等。

基于上述原因，多智能体强化学习中的value- based方法可以被抽象为如下形式：


比如，Nash-Q Learning算法就是利用纳什均衡来作为最优的定义，则上述两部分具体为：

求解当前的纳什均衡:


通过Nash值函数来改良对Q function的估计:


MARL设定中的Policy-based的方法也同样需要做一定的变化来进行适应。显然地，对于多个智能体的环境，其目标函数可表示成图片，利用随机的策略梯度方法进行更新时，具体计算方式为:


其中, 表示第个agent所执行的动作，表示是其他所有agent所做的联合动作。同样地，与单智能体RL相同，可以使用确定性的策略梯度来求解，则计算方式为:


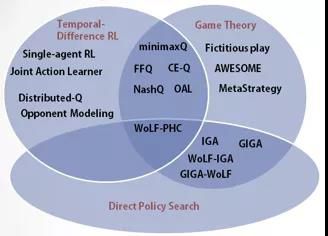
03：经典MARL视角下的分类

天下大事，无外乎两种，一曰合作，二曰竞争，如果有第三种，那就是合作与竞争的混合。在传统的MARL研究中，可以根据任务类型来进行分类。一般来说，最常用的分类方式是三类，第一类是合作任务，比如一群机器人合作完成一个任务，这些机器人彼此之间具有完全相同的目标；第二类是竞争任务，比如很多对抗性的游戏，双方具有完全相反的目标；第三类是混合性的任务，agent之间既具有合作性，又具有竞争性。


另外，也有从学习方法角度来进行分类的。第一种就是我们所熟悉的分成Value-based方法和Policy-based方法以及更加强调博弈论部分的内容。同时，MARL方法也可以利用中心化的学习(Centralized Learning )和去中心化学习(Decentralized Learning)的方式来进行分类。


四. 学习如何合作

01：CTDE

合作任务是多智能体领域经常会面临的问题，主要指智能体一起工作，相互合作，并最大化共享的团队回报。一般会使用Dec-POMDP的方式来进行建模，可以用value-based和policy-based的方式来进行学习17。

使用value-based方法来求解多智能的合作问题，必须解决的问题就是如何建模多个智能体的的值函数。

第一种直接的方法，采用所有智能体联合的网络，中心化的计算总体的值函数Qtot的方式来求解，也就是将所有智能体的状态，动作，奖赏等放进同一个网络当中去，并训练得到一个联合的值函数。显然，这种方式最大的问题就是很难扩大到比较复杂的问题上去，即方法的Scalability有限。

第二种方法完全相反，中心化的值函数难以扩展，就采取完全独立的方式，即去中心化值函数，见图12左所示。与中心化方法相比，显然此方法的扩展性会更好，比如Independent Deep Q-Networks18。但是其突出的问题在于，整体目标如何与个体目标达成一致，个体之间如何分配，即会有比较大的Credit Assignment问题。

第三种方法则结合了上述两种方法的优势，提升扩展性的同时，可以有效地减小Credit Assignment的问题。具体地，每一个智能体保留各自训练值函数的部分，但是在个体值函数之上，增加Mixing Network，完成个体目标与整体目标之间的连接，如下图右所示。基于此，每一个智能体在执行策略的时候，根据自己的局部值函数来选择动作，但是整体的训练又是经过Mixing Network之后的整体目标。


从上述描述中可以看出，第三种方式的主要特点是中心化的训练，非中心化的执行(Centralized Training Decentralized Execution), 也用此特性来命名这种方法，并简称为CTDE。同样地，为了保证联合的目标与个体目标之间的一致性，Mixing Network部分需要做出一定的限制，被称之为Individual-Global Maximization Principle，简称IGM Principle，其数学表达为:


02：VDN 算法

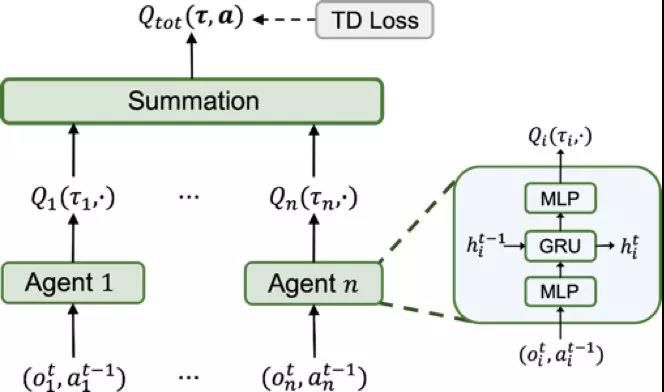
按照CTDE的思路和值函数分解的要求，一个实现简单，使用的也比较多的算法Value Decomposition Networks（VDN）被提出19。VDN在处理多个智能体的值函数时，采用了简单的求和(Summation)的方式，即有下图所示结构：


通过这样一个和的值函数形式，结合神经网络的BP操作，实际上也隐含地实现了多个智能体之间的Credit Assignment。然而，当每一个智能体均取最大值时，他们的和必然也是最大值，但反过来却不一定成立，也就是说，以Summation方式来进行值函数分解，其是满足IGM的充分条件，但却不是必要条件。同时，这也意味着VDN算法的表示能力有所限制，对于不满足Summation这样的充分条件的多智能体情形，就不能很好的刻画。同时，除此之外，VDN在网络结构上还做了更多的设计，使得参数共享，以及各个智能体之间可以进行通信。

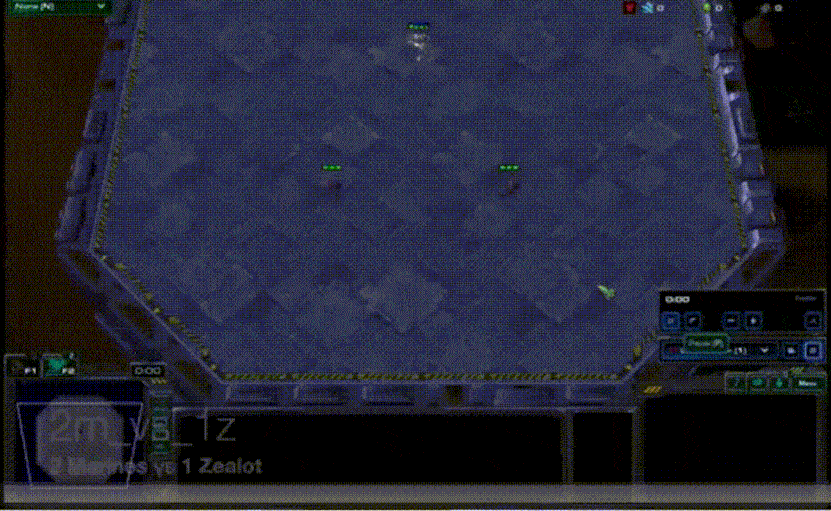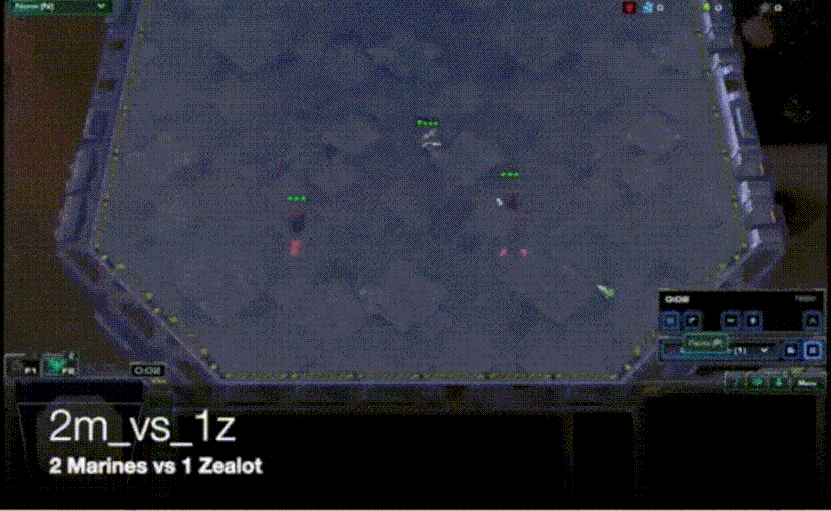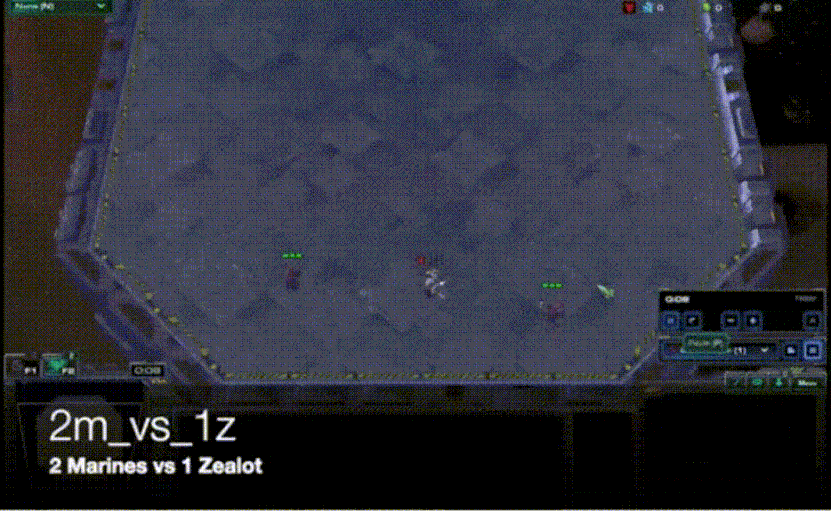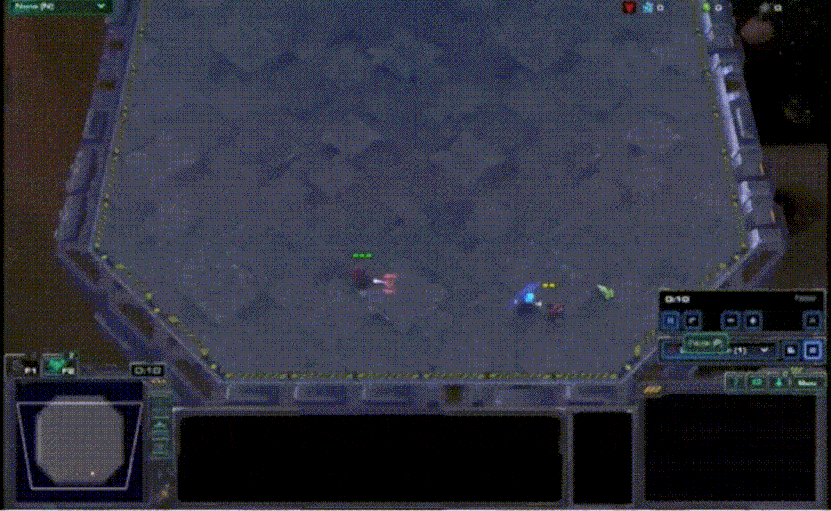
VDN算法虽然比较简单，但是其在众多问题上的表现均比各个agent单独训练要好很多。合作智能体强化学习领域中常用一个测试环境StarCraft Multi-Agent Challeng(SMAC)，其主要是将星际争霸2游戏上的各个子场景拿出来进行训练和对比21。其中的一个子场景是2m_vs_1z，需要让两个海军陆战队与一个狂热者进行对战，直接对战的情况下，两个海军陆战队是无法战胜狂热者的。使用VDN算法在这个场景下进行训练，海军陆战队学会了不断放风筝的技巧，并通过这种方式战胜了狂热者，如下图所示。


03：QMIX算法

除了VDN算法，目前MARL最为常用的算法之一是QMIX算法20。QMIX也是在CTDE的框架下对Mix Network部分进行优化。VDN算法使用了Summation的方式进行中心化的训练，QMIX算法则放松这个约束，并不要求各个智能体与整体的值函数是和关系，而是做了单调性的要求，即图片，以增强其表示能力。

在具体的实现上，QMIX网络中使用了一个方法，在其Mixing Network中，增加一个取绝对值的激活函数，使得所有的权重ω限定为非负。除此之外，其在网络结构其他部分也进行了设计，图 15(b)是QMIX整体的结构，与一般的CTDE结构相同，在各个智能体的值函数之上增加Mixing Network。图 15 (c)表示的是单个智能体的的结构，主要采用了一个DRQN来拟合自身的Q值函数，循环输入当前的观测 以及上一时刻的动作来得到Q值。图 15 (a)就是Mixing Network的结构了，其也将状态st作为输入，输出为混合网络的权值及偏移量。为了实现网络中权重的非负性，采用了一个线性网络以及绝对值激活函数的结构，但是偏移量则没有做非负性约束。


由于满足上文的单调性约束，对Qtot进行argmax操作的计算量是随智能体数量线性增长，而不是随智能体数量呈指数增长。另一方面，与VDN算法相比，VDN算法中使用求和的方式来表示总体与个体的关系，其表达能力显然是比较有限的，而QMIX算法使用的是单调性的限制，其限制更少，表达能力更强。具体地，VDN算法采用的求和方式，是一种线性函数的形式，而QMIX算法采用的单调性要求，是一种单峰形式。以下图 16为例，VDN和QMIX所能表示的情形如第二第三列所示，真实的形状如第一列所示，可以看出，QMIX的表示能力比VDN要强，另外，在第二种情况下，不仅是双峰，还有一个尖锐的峰，则QMIX也不能很好的求解。


同样地，在SMAC上使用QMIX算法进行训练，在星际争霸2的很多场景上取得很好结果，如下图 17所示：


04：基于策略的方法

上面主要介绍了几个基于值函数的多智能体方法，与单智能体强化学习方法类似，多智能体的方法也可以用基于策略的方式来求解。

在基于值函数的方法中，我们主要采取了CTDE的方式来进行训练，以实现规模和效果的权衡。在Actor-Critic框架中，去中心化的执行变得很自然。如下图所示，每一个智能体均维持一个Actor，并完成个体的交互，而Critic部分采取和CTDE相似的处理，使用中心化的训练方式。整体上看，就是中心化Critic去中心化Actor(Centralized Critic with Decentralized Actors), 这也是目前基于策略的合作多智能体强化学习最常采取的训练方式。


这种机制下，考察其训练与单智能体有何不同。在单智能体中，计算梯度的方法可能是图片，而采用Centralized Critics with Decentralized Actors的多智能体，Actor部分多个，有各自的策略(动作)，则梯度计算为图片。与单智能体相似，我们也可以通过增加一个ai无关的的baseline来减小方差，即图片,其中a?i表示除第i个智能体外的其他智能体的动作，以与ai无关，满足baseline的要求。

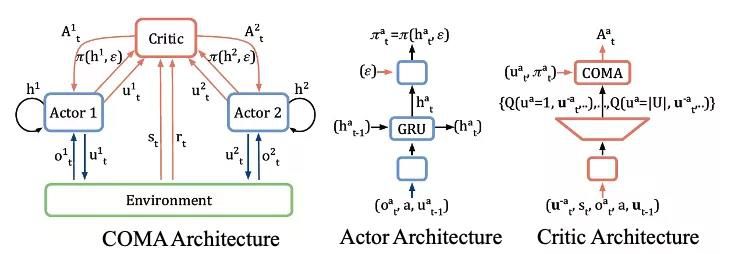
在此基础上，有两个目前相对使用较多的算法。一个是随机性策略的Counterfactual Multi-Agent Policy Gradients(COMA)32，其主要是引入了counterfactual baseline，以起到降低方差和更好的credit assignment的作用，整体结构如下图所示。另一个是确定性策略的Multi-agent Deep Deterministic Policy Gradient (MADDPG)，其可以看作是DDPG算法在多智能体上的扩展33。


五. 学习如何竞争

除了合作外，多智能体中最常遇到的情形就是竞争了，我们这里主要考虑的是zero-sum的情况，比如各种游戏场景中不同团队之间就是这样的零和博弈。这部分讨论如何在零和博弈设定下，不断地提升多智能体的能力，战胜更强的对手。

01：Naive Self-play

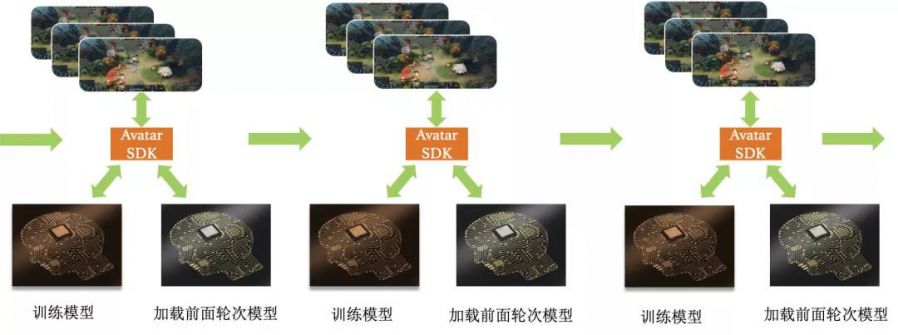
self-play是在这种场景下最常使用的算法之一。Naive Self-play主要指的是，智能体将上一版本的模型作为对手来进行训练，并产生新的模型，如此迭代2。通过这种方式面对不断增强的对手进行训练，可以防止由于巨大的技能差异而导致梯度消失，其流程如下图20所示。这种方式在围棋，象棋和很多其他的游戏中均取得了巨大的成功，比如AlphaGo项目中采用了这种方式来进行训练，Avatar平台上目前也支持了动作格斗，MOBA，FPS等各品类的PvP游戏采用这种方式来进行游戏AI等研发和生产，如下图所示。



从博弈论的视角看，Self-play是一种迭代的求解Best Response的过程。当然，这里使用的是学习的方式，使用强化学习算法加上比较好的参数，得到了针对当前对手模型的近似Best Response，再 继续进行下一轮迭代，持续提升模型的能力，并且每次训练的对手能力不会和自己相差太大，可以有效地增加训练效率。

那么这种Self-play的机制能够适应所有的零和博弈的情况吗，或者说在什么情况下才能成功呢？整体上看，主要有两点：

局部上看，上述每一轮训练中，必须保证训练有效，出现能力的提升，即At+1>At,At>At?1,?

全局上看，要使得上述迭代流程有效，最根本的要求是这是一个Transitive Game，各个玩家的胜负情况必须以完全传递，即：如果有At能够打败At?1，且At+1能够打败At，则一定会有At+1可以打败At23。

02：σ-uniform Self-play和Prioritized Fictitious Self-play

Self-play要取得成功需要满足上述两点要求，第一点是很自然的，我们假设通过良好的算法设计和参数选择，能够使得单轮训练达到目标，这里不再考虑。第二点要求博弈能够满足传递性，目前在很多游戏中使用的排名机制Elo Rating包含了这样的假设。玩家之间不可能都发生过对战，利用这样的传递性就能够实现对所有玩家的能力进行排序。显然，当满足这样的条件时，Self-play可以持续有效的进行，并保证能力不断地提高。

有些博弈能够满足传递性要求，被称为Transitive game，比如关于Good，Better，Best三者的评价以及三者之间的PK，其就是按照整体排序，相互之间的博弈具有完全传递性。一个相反的例子是剪刀石头布博弈，三者之间相生相克，每一个平均收益均为0，显然是无法通过单纯Self-play的方式来提升策略的。


在Navie Self-play的设定中，每次训练都只将最近版本模型作为对手，在存在循环胜负的博弈场景中，可能出现策略退化(strategy collapse)，即训练后期的模型对战靠前模型的胜率会出现下降，甚至下降到打不过的程度。为了解决这个问题，一个很自然的想法就是把历史上的各个版本的模型也加入到对手模型中，与这些模型一起对战训练，以期望能够解决策略退化的问题。

一类经常使用的方法就是σ-uniform Self-play。其主要是将迭代过程中的老模型收集起来，而不是直接丢弃，加入到模型池中，然后在选择对手模型时，给予这些旧模型一定选择比率，使得模型在整个训练过程中不会遗忘对战旧轮次模型的策略。一种简单的策略是，绝大部分对局仍然使用最新模型，而剩余的对局在老模型上进行均匀随机采样。

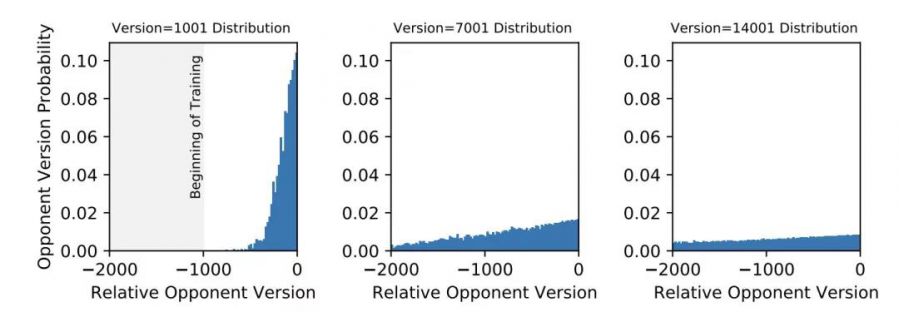
Dota2上的游戏AI OpenAI Five在训练过程中就采用了这样的方式。具体地，其80%的游戏对局使用的对手是最新模型，而剩余20%游戏对局的对手则是在老模型中选择，以增强模型的鲁棒性。不过，对于老模型的选择比例，其继续进行了优化，使用了一个老模型上的动态采样系统。每一个老模型i=1,2,…N,都会被给予一个分数qi,然后对手模型会根据softmax分布来进行采样。当模型被加进历史模型池中时，qi会被赋予最大值，当其输给了当前训练的模型，其分数则会被减少，图片,其中η被固定为常量0.01。可以看出，在这个机制中，绝大部分的计算资源会放在最新的模型上，在老模型中，会把更多的计算资源放在那些当前模型胜率更低的对手模型上，而降低那些胜率很高的对手模型，以尽量做到效率与效果的平衡。

图22展示了OpenAI Five训练早期，对手模型版本号的变化情况。刚开始时，对手模型绝大部分都是很新的版本，而随着训练的进行，其更旧版本模型所占比例呈现越来越高的趋势。另一个角度上，图中的斜率表示了当前训练的模型超过历史版本的速度有多快，在比较靠后的版本中，对手的分布中依旧包含比较多老版本模型，既表明了在初期训练后，学习进程会变慢，也证明这种加入历史模型做对手进行训练的必要性。


Prioritized Fictitious Self-Play是另一类改进方法。其与上述方法思路相近，只是在对手模型的选择方面采取了更加精细化的选择和处理，其是由Deepmind在星际争霸的AI AlphaStar上首先提出并应用的。为了能够能够选择到最有价值的对手，放弃了直接大部分比例使用最新模型的方式，而是完全利用模型之间的对局情况提供匹配信号，根据下式, 针对当前训练的模型，对整体模型池中C的模型B进行匹配概率的打分：图片, 其中，f:[0,1]→[0,∞]是某个权重函数。具体地，可以设置图片，其中x是胜率，p是某个用来调节分布的正数。这种方式使得对手选择时更加注重难的对手，比如图片,即可以100%战胜的对手不会被选择，通过更关注难的对手，要求训练中必须打败每一个对手，而不仅仅只是优化平均表现，这显然对于存在循环博弈的场景更加有效。如果一直与最难的对手打，一方面会使得其他对手缺少上场机会，另一方面难以获得有效信息，也会降低训练效率。因此，在AlphaStar使用的PFSP的结构中，还提出另外一种形式图片, 显然这是在x=0.5时取得最大值的凸函数，而在x=1或x=0时取值为0，即其具有更倾向于选择能力更加匹配的对手，以加快学习效率。

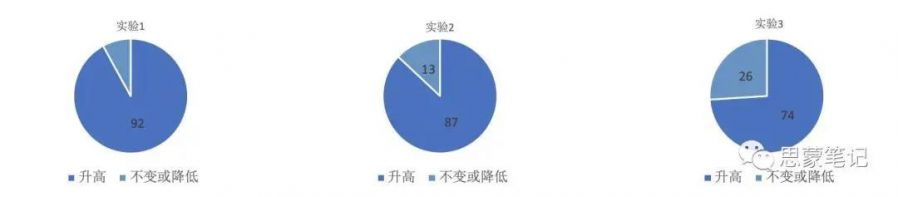
除此之外，在很多游戏中还存着众多不同的角色，阵容，所可能出现的搭配众多，其中也必然会出现较大的不平衡， 从而也会影响模型的训练过程以及最终模型线上的表现。出于此原因，我们在使用Avatar平台进行游戏AI开发时，进一步地针对模型，阵容，角色等进行训练中的匹配调整，形成了如下图所示的流程，在模型方面融合了σ-uniform Self-play和PFSP等各项技术，在阵容调整方面融合了CFR(counterfactual regret )24和PFSP的方法，并使用热更新的方式来进行在线更新，加快训练效率。如下图1所示。经过这样的处理，我们在某游戏的场景中，针对100种阵容搭配进行测试，其中绝大部分阵容的胜率均出现明显上升，整体的胜率均值上升，各阵容胜率的方差有所降低，如下图2所示。



03：Population Play (PSRO与与League)

经过上述优化处理，在很多博弈环境中，已经可以得到很好结果，通过对战历史对手集合增加了鲁棒性，并根据胜率调节具体的选择比例，增加训练效率，减少策略退化。我们通过算法的优化，参数的调整，可以在不少的博弈问题上，能够得到一个模型，可以针对Self-play得到的所有历史模型，均训练得到很好的效果。

不幸的是，我们又有了新的问题。首先，对于完全的循环博弈而言，不存在这样的一种策略，可以打败其他所有策略，比如剪刀，石头，布，到底哪个更好是没有意义的。

次之，假设我们可以训练出完全克制模型池中历史版本对手的模型，是否就完成了我们的目标呢？从监督学习的视角来看，这涉及到训练集和测试集的差异。我们Self-play训练得到很好的模型，能否在真实的博弈空间中发挥很好的作用，取决于当前训练得到的这一批模型的分布与真实的分布差距情况，如果满足独立同分布的假设，那么显然其可以获得比较好的泛化误差。然而，在Self-play的训练过程中，无法有这样的保证。当所有历史模型仅仅分布在真实空间中很小一簇中时，即使训练出来的模型可以打败所有的历史模型，当其遇到空间中 相隔比较远的模型时，依然可能会有很差表现。

最后，从游戏业界使用游戏AI的需求来看，也对其有能力覆盖广，每一个能力段有多种多样风格表现的要求，而不仅仅是某种固定的套路而已，这显然也是单一的Self-play无法完成的。

为了解决上述问题，需要将问题上升一个层次，不仅仅关注单独的博弈本身，而是把视角放在更高的population层次上。我们不必解答剪刀石头布哪个更好的问题，而是从元博弈的角度(Meta-game)上进行求解，并且在population层次扩展探索到的博弈空间，并生产出更加丰富的AI。

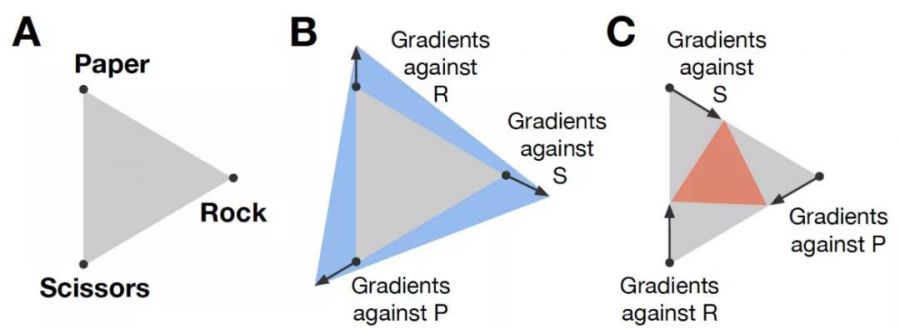
一个有代表性的工作是Policy Space Response Oracle (PSRO), 其实际上是前面所说的Double Oracle在meta-game上的扩展，其所选择的是更高层的策略而不是原始的动作25。使用N个agent的population的进行训练，并且对手使用的是所有对手的纳什均衡策略，如下图1所示。当然，与Double Oracle不同的是，使用Deep RL的算法来求解Best Response，由于使用的是纳什均衡，也被记为PSRON。在此基础上，还有一个改进版本PSROrN, 其区别是选择对手策略时，不仅有纳什均衡的要求，还加上了只选择能打得过的对手，不去考虑那些打不过的。PSROrN,的一个可能好处是使得博弈空间得到扩展，如下图所示，在剪刀石头布的博弈中，当布与石头，剪刀与布，石头与剪刀进行对战时，其博弈空间会从灰色变成蓝色，逐步变大，而如果反过来与自己打不过的那些进行对战，其博弈空间则会从变小，从灰色变成橙色，如下图2所示。然而，这说法目前缺乏理论支撑，在不同的博弈场景下可能有很大差别。



另一个广为人知的使用population play的工作是AlphaStar，其采用了不同的处理方法，称为联盟训练(League Training)。AlphaStar的研发中使用了相当多的技术，包括但不限于利用人类样本做模仿学习初始化，利用人类样本约束后续的学习不要走偏，网络结构的设计与搭配，Off-policy学习的技术改进等等。其中，为了克服星际争霸游戏中较为明显的循环胜负问题，AlphaStar使用了一个全自动的联盟训练框架，联盟一共包含三类智能体，分别是Main Agent、Main Exploiter和League Exploiter，从名字上来看，可以分别理解为是主力选手、开发主力选手弱点的陪练和开发整个联盟选手弱点的陪练，在AlphaStar中，使用了不同的对手采样方式，来训练这三类智能体, 包括Self-play, 不同设置的PFSP，以及他们的组合。通过引入联盟训练的方式，AlphaStar模型在能力上得到了进一步的提升，达到了职业玩家的水平8 34。

04：著名案例简析

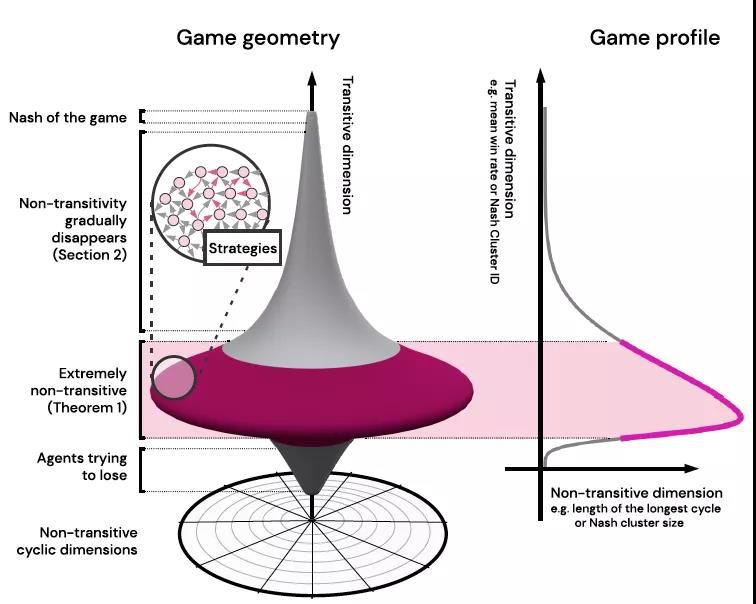
粗略地看，博弈可以分为传递性博弈，和非传递性博弈，在前面均有相应例子。但是，对于复杂的博弈场景，比如很多电子游戏，其更加可能是传递性博弈和非传递性的结合，真实世界则更加如此。

有工作就对复杂博弈场景中传递与循环的关系进行探究，并认为纺锤体是更合适的一个建模和描述26。如上图2所示，高度表示能力的高低，技能的水平，而每一个横截面则表示在此能力下，所采取的不同策略，打法等。在能力很低时，横截面面积小，具有很好的传递性，对应了我们训练开始naive self-play往往也能发挥比较好的效果。随着能力上升，横截面面积逐渐增大，即循环性逐渐增多，这也与我们的认知相似，中等水平的玩家总是互有胜负，且玩法各有特点，同时也使得AI的训练变得更困难，更容易“绕圈”。而当水平继续增高，到达了真正的超高水平时候，循环性就变得很小，找到了博弈中的“最优解”，从而做到”万变不离其宗”。


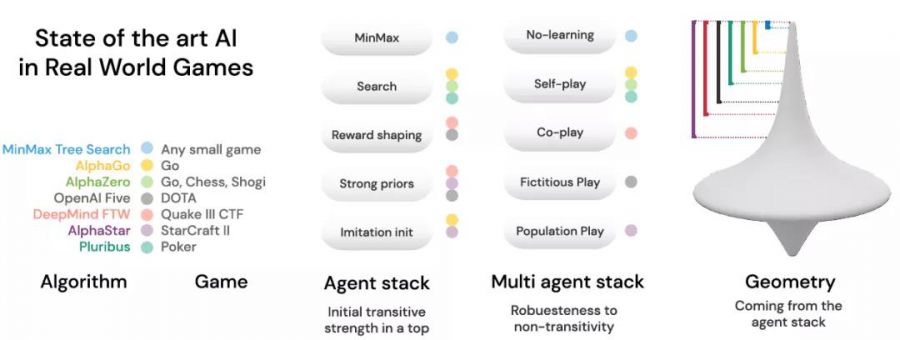
带着上面这样的认识，我们去重新审视目前一些著名的游戏AI案例，整理各自在训练迭代中所采取的方法。引爆这波AI热潮的AlphaGo(Nature)，采用了人类数据来做模仿学习27，获得了一个很好的初始化(imitation init)，并结合了蒙特卡洛树搜索的方法优化效率，最后再使用Self-play进行强化学习的不断迭代，以将其提升到超越人类的水平。AlphaZero则在此基础上完全去除了对人类数据的依赖，完全依靠强化学习训练，并实现了在围棋，国际象棋，日本象棋上的通用性。Dota2上达到很高水平的OpenAI Five，在神经网络设计上进行了精细的设计，以实现团队中五个英雄的信息共享和目标一致。同时在奖赏工程中做了非常多细致的设计和参数调整，融入了人类先验知识，在迭代过程中，没有简单使用naive self-play，而是将历史模型也放进对手模型池。星际争霸2游戏本身策略更加复杂，且不同的种族，不同的策略之间存在明显的循环胜负关系，因此在AlphaStar的设计中，不仅使用了人类数据来做模仿学习的初始化，还在后续强化学习的训练中继续基于人类数据的统计量对模型进行约束，更进一步，其使用了pupulation play的方式来进行训练，以提升模型的鲁棒性和能力上限。


六. 游戏AI中的应用与展望

01：游戏与AI

游戏与人工智能技术一直有着非常紧密的关系。自电子游戏诞生之后，人工智能研究者就把电子游戏作为测试人工智能算法的一个理想的环境。这里面很重要的原因是，很多电子游戏，尤其是棋牌类的游戏，都是被人类规则良好定义的，蕴含着人类智能的基本要素。因而在人工智能发展的早期，绝大部分人工智能的研究者都在努力做出一个很厉害的机器人可以在电子游戏中战胜人类29。在最早的时候，图灵和香农就尝试使用Minimax 算法来让AI下棋，强化学习+自我对弈也很快被Arthur Samuel应用到跳棋(Checker)中28。

随着深度学习在近几年取得的突破性进展，人工智能正在深刻的改变着安防、金融、医疗等领域，那么在千亿美元规模的游戏行业，人工智能技术同样可以发挥其作用。同时，现代的游戏中，越来越多的呈现出多人对抗，多人组队等特性，以提升其趣味性，或者存在着大量的游戏内的小怪，Boss来作为游戏的关卡。这些具体的场景使得游戏业界内一直会有设计比较好的游戏AI的需求，以快速生产游戏中的大量高质量智能体。

智能体控制，指的是游戏中的玩家和非玩家角色的控制，这里的角色控制，广义上包括角色的剧本、台词等，而狭义则指角色的游戏行为(gameplay)，传统游戏AI的做法是通过规则驱动的思路来实现，即设计出角色在不同情况下的行为逻辑，再通过角色控制的接口，配合动画