一种游戏体验曲线的拆解方法

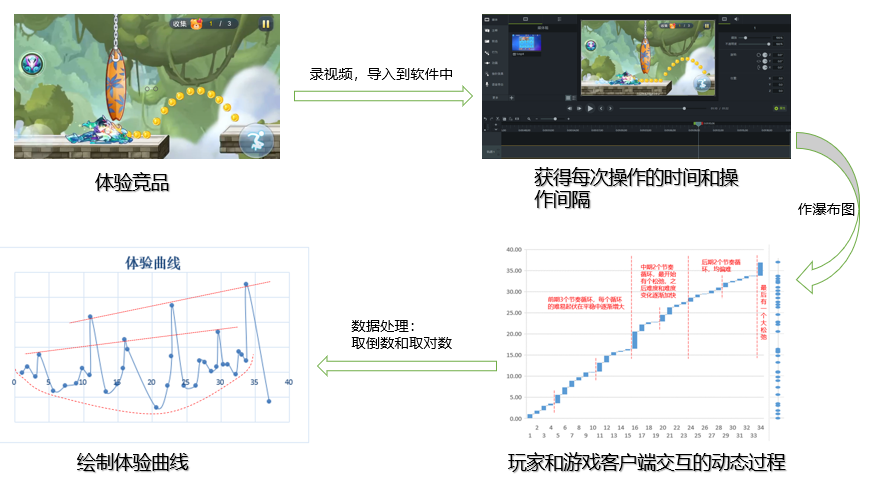
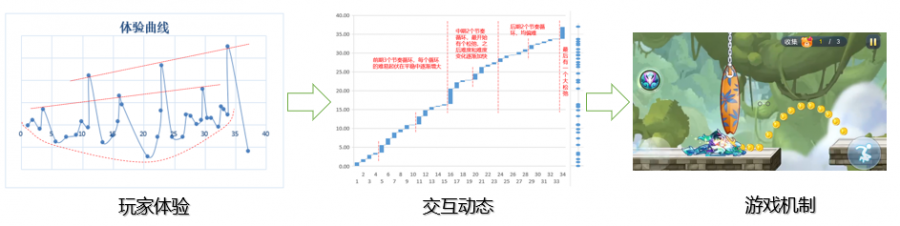
本文以天天酷跑的关卡设计（第一关）为例，描述了从游戏机制，到玩家和客端的交互动态，再到体验曲线的拆解过程，本过程适用于跑酷/竞速/飞行射击/平台跳跃等类型游戏的拆解，主要流程如下：


一、获得原始数据


通过竞品体验，录制视频，导入软件获得精确的操作时间，最终得到原始数据。


二、玩家和游戏交互的动态过程


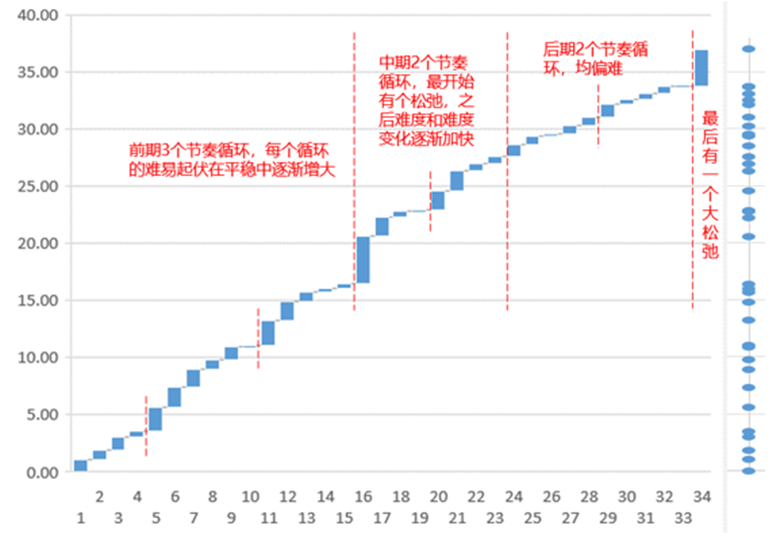
瀑布图说明：

• 横轴为第几次操作
• 纵轴为游戏时长
• 右侧打点为操作点，与游戏时长对应；
• 图中的蓝色矩形为操作间隔，两矩形之间为一个操作点。
  

瀑布图虽然可以相对更多的包含数据中的信息，但还存在两个缺点：

虽然可以发现一些规律（红字），但可读性不强；

只可以表现出一些局部规律，整体规律比较难表现。

总的来说，这张图更多是用来展示玩家和游戏客户端交互的过程，而无法很好地表现玩家体验变化。

三、数据处理-对体验进行量化

首先将用户体验简单地定义为紧张和松弛。两次操作之间的间隔越短则越紧张。

Step1：将所有的操作间隔转化成倒数：y=1/x


原因：

• 与紧张体验建立正相关的联系。操作间隔越短，则紧张的值越大，因此将操作间隔转化成倒数，倒数值和紧张感是正相关的。
• 操作间隔的大小变化和紧张感的体验变化并不是线性相关的。将操作间隔转化成倒数，更符合规律。
  

Eg.假设有三个操作间隔5s，1s，0.1s。5s和1s相差了4s，但带给玩家的紧张感变化不大；1s和0.1s虽然在数值上仅相差0.9s，但带给玩家的难度挑战变化却是远远大于前者的。

假如对以上三个数值取倒数，即：0.2，1，10，，显然取倒数之后可以更准确的描述体验变化。

Step2：对所有的倒数取对数：z=ln(y)


原因：

• 为了将数据展示在同一个坐标系上，对所有倒数取对数。因为取倒数之后，最大值和最小值相差较大。
• Step1取倒数的操作一定程度会抹平松弛状态的规律（操作间隔较大的数值），倒数取对数之后可以使规律更明显。
  

Eg.假设有三个操作间隔5s，1s，0.1s。

假如对以上三个数值取倒数，即：0.2，1，10；5s和1s原本有较大的差值，取倒数之后差值变为0.8，原有的规律则可能会被抹平。当继续对倒数取对数时，三个数变为：-1.61，0，2.3，差值变为1.61，且与最大值的差值变小，会使规律更明显。

经过Step1和Step2的处理，最终可以将体验量化为数值z。

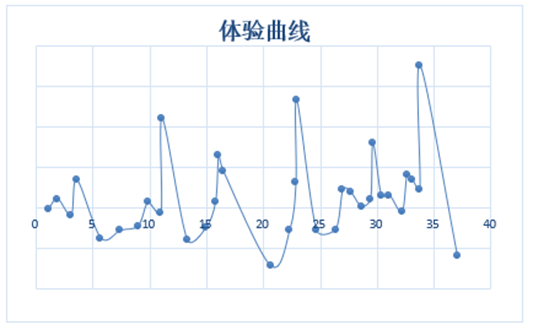
四、绘制体验曲线

以游戏时长为横坐标轴，最后获得的对数z为纵坐标轴，绘制图像。

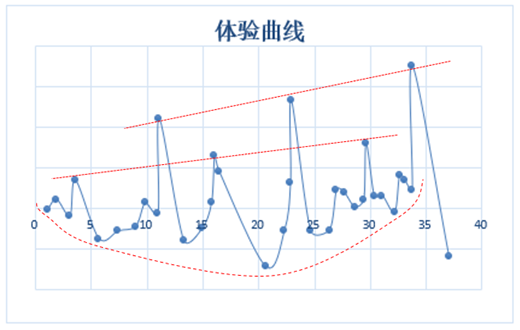
• 在紧张体验上给玩家带来3个大高峰，3个小高峰，且每个大高峰之前都有一个小高峰；
• 同类高峰出现的各个间隔相差不大（<1.5s）;根据斜率，大高峰紧张感增长速率大于小高峰的增长速率；
• 共有2个松弛的大低谷，分别出现在游戏时长的中部和末尾，这也是玩家最爽的2个阶段；
• 以中部松弛大低谷为中心，松弛的分布呈U型，且右侧相对左侧更紧张（除去末尾的大松弛）；
• 中部的3个松弛低谷处，即使操作失误，也不会造成游戏失败；且相对较小的2个低谷和大低谷相差较大，突出中部大低谷带来的爽快感。
  

五、参考作用

逆向进行之前的过程，先根据拆解的结论设计体验，接着从体验推导出玩家和游戏交互的动态变化，最后推导出我们想要设计的游戏机制。


六、过程评价

缺点：

• 体验过程受到体验者个人因素的影响，如体验者的手速/反应时间等，可能和设计者原始的设计有一些偏差。
• 将所有的操作都简单的归类为相同的动作，没有考虑不同操作之间的难度差异。
• 只可以量化操作，无法量化策略，主要适用简单的跑酷/竞速/飞行射击/平台跳跃等类型的游戏。
• 数据处理过程中利用了1/x和ln(x)这两个函数，可能有更优的选择。
• 只可以得到竞品设计时的边界和规律，无法反拆出竞品更细节的设计思想。
  

对应的优化思路：

• 定义一个标准的玩家能力之后，对数据进行微调
• 给不同的操作赋权重
• 暂无
• 暂无
• 暂无
  

（欢迎大佬们challenge以上步骤or一起讨论可优化的点(*╹▽╹*)）


来源：River的博客
原文：https://mp.weixin.qq.com/s/z0CvINRXfSQ938Ln7tKulg