这次主要接着
上一篇文章继续往后谈,涉及暴击、穿透、乘法公式下的防御和减法公式的问题。
下一篇的话,打算试着引入MP和魔法攻击这种。我也不知道自己到底会在哪一步彻底把问题变成我解决不了的程度,姑且现在先往前推动一些吧。
暴击
即使我们在伤害计算时引入了乱数补正,保证每次伤害都会打出不一样的数值,以此来增加刺激感。然而对玩家而言,这种数值的增加并不明显。即使偶尔运气好一次,也最多只能打出乱数补正的上限伤害,然而为了保证游戏的数值相对稳定避免运气压倒一切,频繁触发的乱数补正自然不会将上限调得很高,充其量也就是在10%上下浮动。
因此,一些游戏做出了暴击这一设定。一些说法认为最早的暴击出现在桌游,而我对桌游完全不熟悉,只听说过DND的D20之类的东西,所以也无法对这个消息的准确度进行判断。不过,DND里面行动的掷点数这一随机过程,倒确实与暴击这种全随机的判定机制非常吻合,考虑到DND对RPG这一品类的深远影响,这一看法多少还是有些可信度的。
就此打住,我们依然还是设定两个角色A和B,但这次我打算在其中引入多段暴击——例如:
生成一个0-100范围内的随机数。
如果这个值大于80,判定触发一次普通暴击,打出1.5倍伤害;
如果超过95,判定触发一次特殊暴击,打出2.5倍伤害;
如果超过99,判定触发一次超级暴击,打出4倍伤害……
当然这个数值设置的是否合理暂且不谈,我们应该看到,决定一次暴击最重要的为两个参数,即暴击率(
![]()
,下文缩写为
![]()
)与暴击倍数(
![]()
,下文缩写为
![]()
),前者决定一次暴击判定为成功的概率,后者决定这次暴击判定成功时,这次伤害应该增加的倍数。
设两个角色A(Health=
![]()
,Attack=
![]()
,CSR=
![]()
,
![]()
,
![]()
……,CM=
![]()
,
![]()
,
![]()
……)和B(Health=
![]()
,Attack=
![]()
,CSR=
![]()
,
![]()
,
![]()
……,CM=
![]()
,
![]()
,
![]()
……)。注意到,当某次暴击判定成功时,其攻击力变为
![]()
,而对应的暴击率为
![]()
。
在这种情况下,由于暴击的随机发生可以极大地影响整个战斗的局势,自然无法仅凭一次简单的互相攻击就能判断两者的战斗力大小。因此此时的战斗力更多地作为一种统计学意义上的战斗力,也就是说,如果A和B互相攻击足够多次数后,战斗力高的一方胜率要高于战斗力低的一方。
通过概率论知识我们不难得知,此时伤害的期望值为:
注意此时出现了下标为0的项,这是因为一次暴击判定必然存在失败的可能性(否则刀刀暴击也就失去了设计暴击的意义)。我们定义:
这样,整个伤害的期望值就可以化简成如最开始的式子一样简洁清晰的形式。
与HA体系相比,不难看出,此时伤害由原本的攻击值变成了结合暴击倍数的期望值,考虑到这时战斗力的统计意义,不难得出:
类似地,在考虑防御力后,战斗力的期望大小应该变为:
穿透
防御的引入固然使得游戏增加了一些变化,但仅靠着生命、攻击和防御这三者做出的数值体系还是太过单薄。据此,我们在这里引入穿透(Penetration)属性用来削减对手的防御力。
此时的伤害公式应变为:
展开括号,则变成了:
这里我们似乎可以把攻击力和穿透两个数值叠加,作为一个虚拟的攻击力数值进行后续的运算。
然而问题恰恰出在这里。
注意到在HADa体系里,一开始的假设即默认“防御低于所受攻击,即攻击必定产生伤害”。在仅有防御的前提下这一问题还不算太突出,因为仅有防御一个限制,在设计时就可以尽量压缩防御值的大小避免这种情况——然而当引入穿透后,事情乱套了:
如果角色A拥有5点防御,但B拥有10点穿透和10点攻击,按照上面的公式,伤害似乎应该为:
然而实际上,10点穿透打在5点防御上,意味着这10点穿透中有5点是溢出的。换言之,实际上的伤害应该为:
这便是问题的根源了。
当然看到这里,这时候有人一定会觉得“那就把穿透也设置得更小,避免这种溢出的情况就可以了嘛”。然而防御值上限已经被压缩的情况下,继续压缩穿透值上限,穿透对玩家的提升就实在太小了。另外还有一个问题——穿透值有溢出的可能而攻击力没有,同样提升的前提下(穿透或攻击增加一点,在不溢出的情况下反映到伤害上都是增加一点伤害),为什么我要去提升穿透呢?直接攻击一路碾过去岂不是更简单粗暴?
这种情况下,穿透就处在了一个很尴尬的位置,相当鸡肋没有什么重要性,但凭空多的这个数值又会分散玩家的注意力,且投入很可能没有收益(比如穿透数值已经比其他角色的防御高的情况下,再投入穿透并不会增加玩家在实际战斗中的优势),而玩家加点尝试发现穿透的问题后,大概率又要回头来喷策划……
这便是减法公式和乘法公式的根本问题了……
当然,这个我会放在下一小节讨论,这里还是先给出考虑穿透情况下的公式:
减法、乘法与除法公式,以及乘法公式下的防御
简而言之,两者最主要的差别在于:
减法公式很容易产生负数,而乘法公式的本质确保了负数很难出现。
原因很简单——诸如伤害计算,防御判定等内容如果用减法公式做,就必然会涉及减法,而初中数学已经告诉我们,两个正数相减,结果可以是正,也可以是负。
负数是一个很烦人的东西。仍然以防御为例——角色A攻击50,角色B防御60,假如我们在一开始的伤害部分偷懒没考虑到溢出的情况,战斗的结果就会变得匪夷所思——A打B,B不仅毫发无伤,随着A的攻击反而一点点奶回来了。这种情况下该怎么写一个稳定的计算公式?毕竟公式不是代码,不可能套几个if或者switch就扔那里不管了。这也是为什么一些策划对减法公式避之不及的原因。
而假如我们把防御变成“抵消20%的伤害”,A攻击B,伤害则变成了40。如果A的攻击变成了5,依然能造成4点伤害。无论A的攻击有多低,其攻击力也必定大于0。原因就在于两个正数相乘结果必然为正。乘法公式正是靠着这个特性规避了负数的出现。
另有一种公式,也是我刚才闲着无聊谷歌翻出来的——除法公式,最简单的形式下,它定义伤害为:
此时战斗力公式为:
除法公式的防御力权重被进一步放大了,如果一个角色的防御力变成0,这个角色等于毫无还手之力,因为此时即使是路边的一只史莱姆,造成的伤害也是无穷大。另外,在这种体系下,防御力的上限不能设置太高,即使防御力只有5,反映到伤害上也已经相当于80%的减伤。而即使防御力的上限提高到攻击力上限的仅1%,在后期属性达到天花板的情况下也相当于一次仅能造成一百点伤害——我想应该没有人会给一个游戏后期的角色设计低于1000的生命值上限……
除法公式也许我之后会再转回来写……到时候再说吧——这里还是先给出乘法公式下的战斗力公式:
其中
![]()
为减伤率,用来抵消对应百分比的伤害。
最后说两句——
最初想写这个是因为想研究一下为什么自己高战力还总是吃瘪,不过现在看了一下,大概也明白了。这种战斗力计算公式,其实很多时候只能起到一个指示性的作用,并不能真正说明两个角色互打,战力高的就必定获胜——但总的来看,战力越高,在不同战斗中获胜的可能越大,这一点是无需置疑的。正如我在上一篇里面举的例子——A(Attack=5,Health=10)和B(Attack=6,Health=10)互打,先手必胜,然而让两个人打一个2攻26血的怪物,不考虑乱数补正的前提下,无疑B必胜而A必败。回合的不连续性使得战斗力这一在连续的前提下推导出的结果显得漏洞百出,毕竟从来没听说过0.5回合这种东西。
下一次除了开篇提到的魔法攻击用来一点点过渡到多元素伤害以外,速度也值得好好考虑一下了——虽然实际上,目前还是逃不开“你砍我一刀我砍你一刀”这种站桩互砍的模型……
作者:老咸鱼
专栏地址:https://zhuanlan.zhihu.com/p/108933100

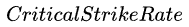 ,下文缩写为
,下文缩写为
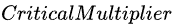 ,下文缩写为
,下文缩写为
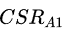 ,
,
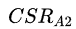 ,
,
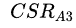 ……,CM=
……,CM=
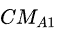 ,
,
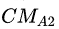 ,
,
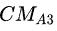 ……)和B(Health=
……)和B(Health=
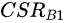 ,
,
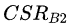 ,
,
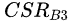 ……,CM=
……,CM=
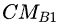 ,
,
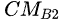 ,
,
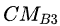 ……)。注意到,当某次暴击判定成功时,其攻击力变为
……)。注意到,当某次暴击判定成功时,其攻击力变为
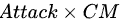 ,而对应的暴击率为
,而对应的暴击率为
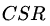 。
。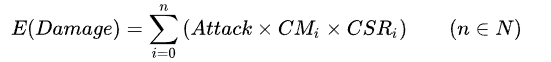
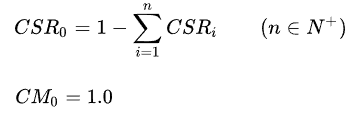
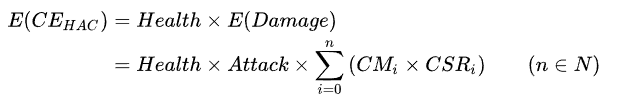

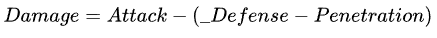
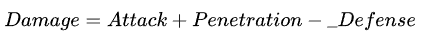
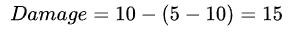
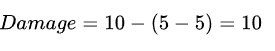

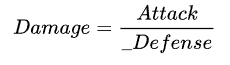
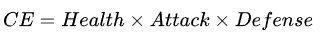

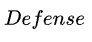 为减伤率,用来抵消对应百分比的伤害。
为减伤率,用来抵消对应百分比的伤害。