本文首发于微信公众号开放世界设计研究所(ID:OpenWorldDesign)
介绍
游戏中的空间为游戏的规则和系统提供了语境,并且作为游戏的演出效果的媒介。在设计游戏空间时,有时我们会以纯粹的空间设计上的术语来思考设计师需要在特定的游戏空间中实现什么。
对于FPS游戏来说,使用自己最喜欢的原型开发工具包去绘制走廊和房间,这通常是灾难的根源。当你尝试去
使用现实中的规则创建游戏空间时,很难设计出有趣的空间谜题。不信的话,你可以想一下,多少个办公大楼摆在一起会很有趣呢?
而元素设计则是一种应用了图形理论,以此进行对各种类型的游戏空间概念化和迭代微调的方法。这种理性的设计方法是一种
无需考虑空间本身的代表元素而去设计空间的方法。本文仍然承认平面图的重要性,不过,我们需要更好的工具来帮助我们创建这些前所未有的东西。
本文将研究从图形理论领域中收集的一些有用的工具,设计人员可以使用这些工具来概念化各种游戏组件,而本文的后半部分将研究这些工具的实际应用。通过这样做,我们将研究一个关卡设计的迭代是如何从这种抽象的实现空间的方法中获益。
图形基础
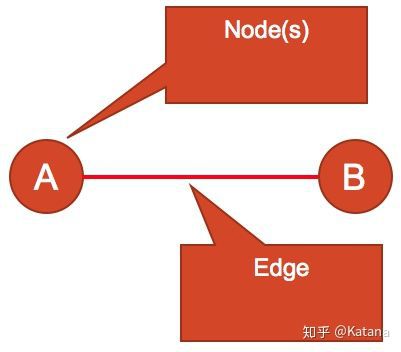
虽然图形理论是一个广泛且丰富多样的数学领域,但本文所讨论的图形可以用来解释空间关系。解释空间关系的图(Graph)的核心是节点(Node)和边线(Edge)(图1)。节点可以用来表示游戏空间/房间、拾取物、出生点和AI的路径节点,边线定义了节点之间的关系。
图1
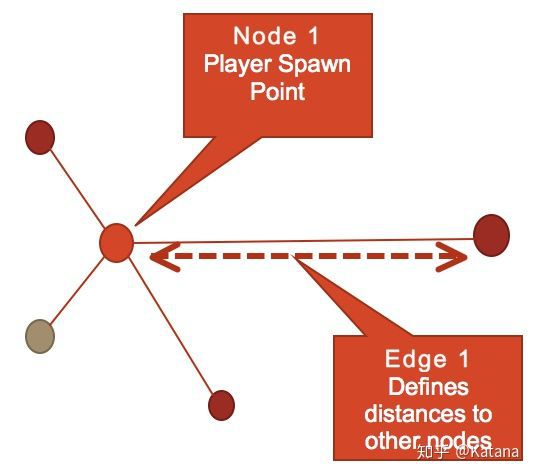
图2是一个由多个节点所组成的简单元素,由边线所连接。在这个例子中,我们在玩家的拾取物周围定义了一组标记。这是一个使用图形方法对空间的文字描述。节点通过边线来连接,这些边线定义了玩家和其他节点之间的最短距离,可获得的代币越多,边线则应越长。
这种方法对于PvP的游戏来说非常有效——
创建一个具有大致相似的道具分布的游戏空间,以此实现游戏的平衡。重复和旋转一个元素将会导致整个游戏空间的对称分布。边线是定义关系的抽象方式,但不一定是走廊或者任何其他的关卡几何体。为了进一步解释这一点,我们需要看权重边和有向边。
图2
我们可以
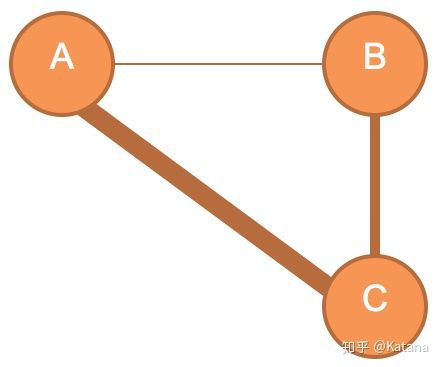
操纵边线物理上的外观,以此帮助在节点之间传递不同类型的关系。在图3中,节点A和C之间的边线比其他节点厚。如果我们使用图形理论来创建空间,并且节点代表特定的游戏空间,那么较大的边线并不意味着两个节点之间的空间更大,而是意味着更为直接的路径。
图3
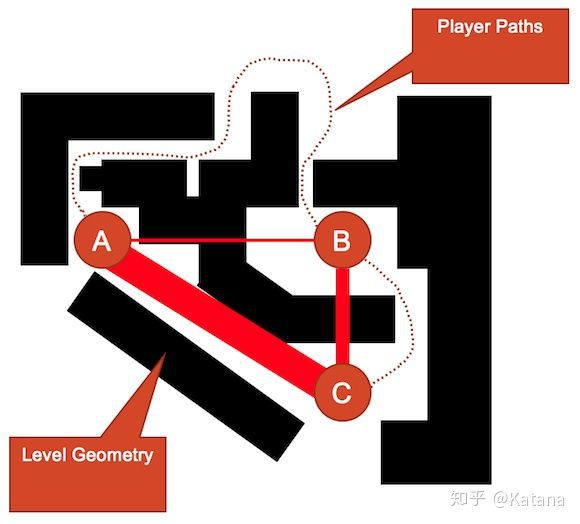
图4从图3中提取了我们的元素,并且使用了加权边线作为指定放置的关卡几何体。在本例中,权重较高的边线在节点A和C之间创建了一条直接且不受阻碍的路径。另一方面,连接节点A和B的权重较低的边线表示会创建出一条自然界中复杂蜿蜒曲折难走的路径。由此示例中足以看出,边线并不直接描述几何,而是描述了节点之间的关系。
图4
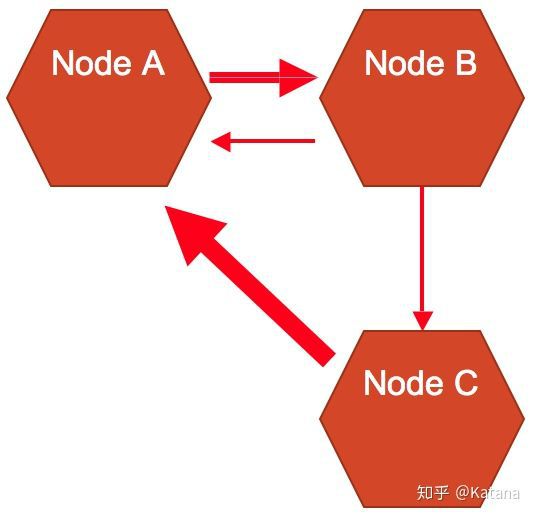
我们可以通过对边线增加方向来进一步的增加边线之间所传递的信息量。图5是一个有方向的边线和加权边的图形示例。图5使用了有向边和加权边获取了在节点A和节点B之间两种不同的传递方式,较厚的边线比另一个更为直接。连接节点B和C的是一个单向门,而连接节点A和C更厚的边线则是另一个单向门,该边线的厚度显示了节点之间的连接且不受阻碍的关系。
图5
节点和边线几乎可以用来表示游戏关卡设计中的任何特征。例如,我们可以使用这样一个系统,即线条所蕴含的权重告诉了我们在节点间抵达目标节点的困难程度。利用边线来描述垂直空间,可以说节点C是地图的最高点。然后,节点C在只能在从节点B出发的意义上说是可传递的。节点B和节点C之间的单向方向可以通过在节点B处所具有的“跳板”来实现,该跳板指向节点C,而不是相反的方向。因此设计师和他的团队可以自行决定为他们特定的元素系统所定义一个具体的表现方式(或唱或跳或RAP抵达目标点)。
为了进一步的解释
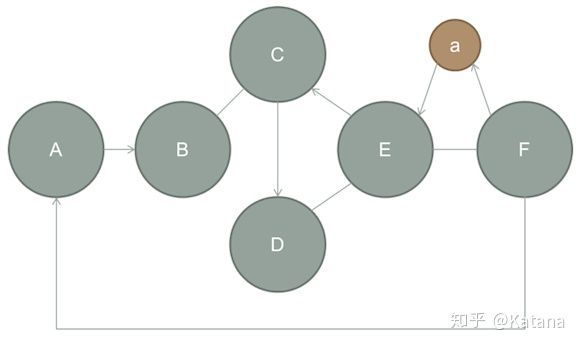
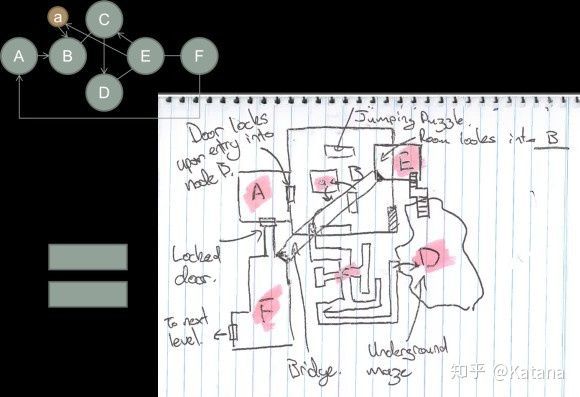
如何使用空间元素来创建游戏空间的概念,让我们考虑一个元素示例,它应该如何实现,以及又不应该如何实现。图6所示的元素是一个简单的空间元素,它定义了一个线性的关卡进展,适用于单人类型的地图。本例中未使用加权边线;但是使用了有向边线从而创建了一个有趣的空间谜题。
图6
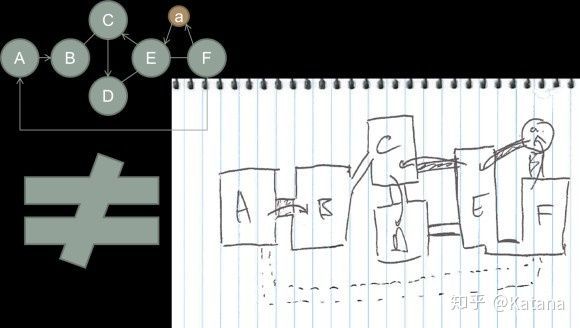
图7则是一个与空间元素无关的例子。使用了基于元素方法的原因是
为了让你的创作过程从纯粹的空间思维中解放出来,转而去考虑创造更多有趣的空间关系。尽管图7中的平面图遵循了元素的空间关系,但它仍然是一个无聊的线性空间。
还有一些其他的缺陷也说明了为什么基于平面图的角度去设计地图是有问题的。首先,在平面图上的线性关卡中,室内逐个房间的布局是在平面空间中绘制地图的直接产物。当你的想象空间是二维的,你的地图也将是二维的。因此,这将会没有有趣的垂直空间,更重要的是,从地图的开头便无法清楚看到目标。
图7
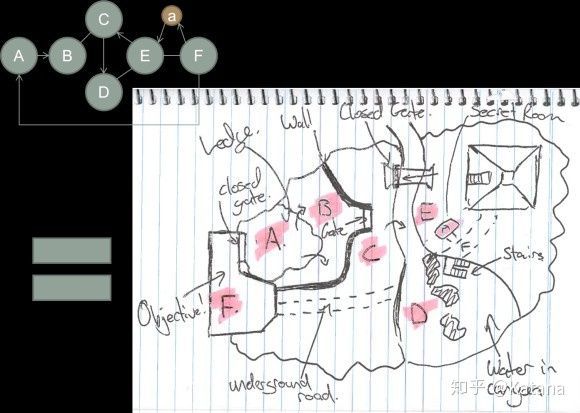
图8是同一空间元素的更好的实现。该示例将每个节点视为一个“玩家空间”,并使用元素的边线来定义这些玩家空间是如何相互作用的。下面是一个假想的游戏区域:
在本例中,玩家从一个可以俯瞰山谷(区域A,该节点同样也可以作为关卡构图中的观察点)的壁架开始。在他们旁边,他们可以看到游戏区域F,这是一个耸立在环境之上的大型人造结构。很明显,这是最终目标点,它的大小和规模立即迫使玩家渴望知道他们如何才能进入结构中。玩家注意到了高塔的入口被锁住了,但他们可以看到远处的另一个建筑,地图E部分的一个大金字塔。金字塔有一个巨大的入口,吸引了玩家的注意力——它是景观中唯一的其他主要兴趣点,因此可以吸引玩家前往。
在区域A和金字塔的起点之间,玩家看到了许多他们需要克服的障碍:一堵巨大的墙面、一座大门紧闭的桥和一个充满水的峡谷。玩家将有时间从高处去观察地形并且获得态势感知。从区域A开始,玩家开始着手去规划他们具体的路线。
玩家从区域A的高架平台上跳了下来——那么这里是一个单向门。在区域B,他们需要进入敞开的大门。最初他们会被顺利吸引到穿过峡谷的桥上,但他们很快意识到它被封锁了,只能从另一边打开。在靠近桥的地方,玩家将注意到有一段岩石可以用来跳入下面的河里而不至于受到伤害。
一旦进入河中,它们会沿着河流的游向从而朝着一个大的开放区域所移动。在这里玩家将找到一组楼梯,将他们带到包含金字塔的高原上。一旦进入金字塔内部,就会有一条地下道路连接到区域F的目标。一旦他们靠近区域F,那么这条道路将在他们的背后所坍塌,因此它得以充当单向门。
隐藏的房间“a”连接了区域F和区域E,但是它也是单向门,只能从F进入。进入后该房间将被洪水冲垮,导致其与区域F隔离,并且迫使玩家回到E部分。
F部分是玩家的目标,进入该区域后,玩家可以继续前进。请注意,由于房间"a"是单向通道而F区则是封闭的,因此这将不再允许玩家回到开放区域。
图8
图9则是对同一元素的另外一种解释,这次则使用了更传统的基于房间的设计方法。
在这个游戏中,玩家从区域A开始,区域A是一个大房间,有两扇门,一扇开一扇关。玩家通过唯一开着的门后得以进入一个巨大的竞技场区域——区域B.这个房间里有一扇门,但是它被挡住了,以至于玩家知道它坏了,他们无法通过。在B里面是一些集装箱,玩家需要在这些集装箱之间运用跳跃能力跳出房间。
在这个高大的房间上方则是一个门框,悬挂在地板上方。玩家还可以看到俯瞰竞技场的房间——区域E。玩家从一个集装箱跳到另一个集装箱,慢慢地探索着垂直空间。一旦到达最高点,它们就会进入一个小型的服务隧道网络(区域C),然后逐渐下降。
在这里穿过隧道后,玩家会下降到一个多层区域—D区。从这里开始,他们可以通过楼梯在D区和E区之间穿行。一旦进入E,他们就可以越过他们先前看到的吊桥,达到他们的目的。在去F的路上,他们注意到顶端皮卡,它位于一个他们以前无法通过B区进入的集装箱上。如果他们的玩家决定跳到这个集装箱上,那么他们需要通过B,C和D进行回溯。
在隧道中经过导航后,玩家可以进入到一个户外区域-D区。从这里,他们可以通过楼梯在D和E之间穿行。 一旦进入E,他们就可以越过他们先前看到的吊桥。 在前往F区的途中,他们会注意到一个拾取物,该拾取物位于他们先前无法通过的前往B区访问的集装箱上。如果玩家决定跳下该集装箱,则他们需要通过B,C和D进行回溯。
图9
图8和图9展示了如何创建一个基于元素的平面图是创造性地解决空间设计问题的极好方法。这种概念化的方法迫使设计师在关卡设计的平面图阶段得以能够创建出有趣的空间选项。根据我自己的经验,
从平面图阶段开始去设计关卡往往会导致非常无聊、且线性的关卡进展,这就是试图在纯粹的二维创意空间中创建有趣的三维空间的结果。
更高级的工具集
既然我们已经讨论了图形理论的基础知识,现在是时候继续研究设计师在设计游戏空间时需要掌握的一些工具了。需要注意的是,这些只是一些可供设计师使用的概念。由于这篇文章占用了其中的一些思想,有些情况下有必要偏离对这些概念的一些纯数学上的解释。本文将探讨以下图形概念:
- 多米诺理论(Dominion Theory)
- 斯坦纳点(Steiner Points)
- 生成树(Spanning Trees)
多米诺理论是一种得以理解节点是如何产生影响范围(AOE)以及该AOE是如何与其他的节点重叠的方法。此工具在从玩家体验的角度上去分析现有地图时特别有用。使用此方法,每个节点表示“游戏区域”和每个空间内所发生的
游戏体验强度。
这种“游戏区域”的概念最初是在《半条命》的设计过程中所探索出来的,其被称为“
体验密度”。体验密度是Valve的设计师在“ 半条命”的创造期间所创造的一个术语。
该概念指的是其认为游戏体验是基于距离,而不是基于时间的。基本的思想是,应始终让玩家来选择进入游戏体验的下一部分,如同现实中在游乐场所游玩时,自由的去选择所需的体验区域。
他们应该得到尽可能多的时间来收集战利品和自由的探索,或者在被放置在高强度游戏体验的状况下进行简单的探索。
图10
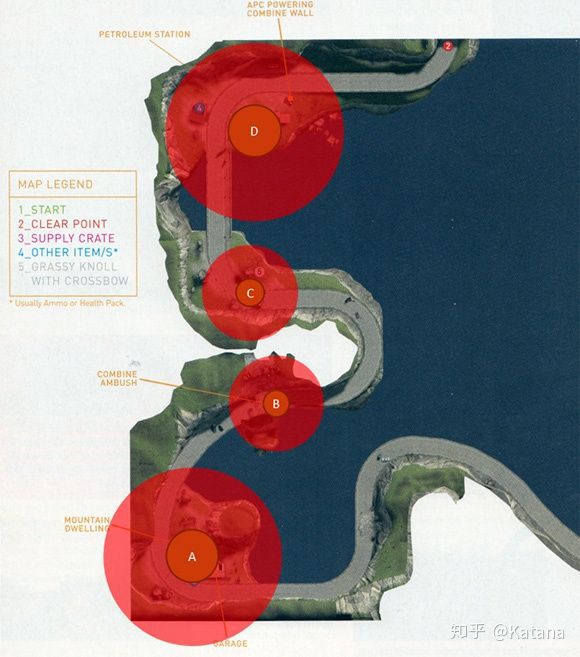
图10是取自《半条命2》中的一个示例,该示例演示了多米诺理论是如何被用于提升体验密度。在此地图中,我们有三个不同的高强度游戏区域,分别由节点A,B和C来表示。节点周围的作用区域旨在于用来表示每个区域的游戏强度。 AOE越大,给与玩家的挑战则越大。
如果我们在设计时考虑到体验密度,则可以使用Dominion来确保不强迫玩家进入连续的高强度游戏区域。从字面上的意思来看,我们正在研究元素设计,以确保我们在各个区域之间,得以为玩家提供足够的情绪体验上的“冷却”时间。我喜欢将这些"冷却"区域想象成为音乐的动态。音乐家兼作家大卫·皮诺(David Pino)在他的《单簧管和单簧管演奏》一书中很好地总结了这一概念:
这样想吧:如果你从岸边眺望广阔的海洋,可能你很快便会感到厌烦。但是,如果一艘有趣的船突然出现,这将使海洋变得生机勃勃,那么视野更可能引起你的注意。同样地,如果你的视野里突然铺满了数百艘船只,那么其中的任何一个都不会引起人们很长时间的关注。同样的原则也适用于音乐的表现:如果听众没有察觉到任何微妙之处,他就会感到无聊;如果他除了这些微妙之处以外什么都没发现,那么他就会感到迷茫和无聊。任何音乐作品中最重要的元素便是它的节奏感。
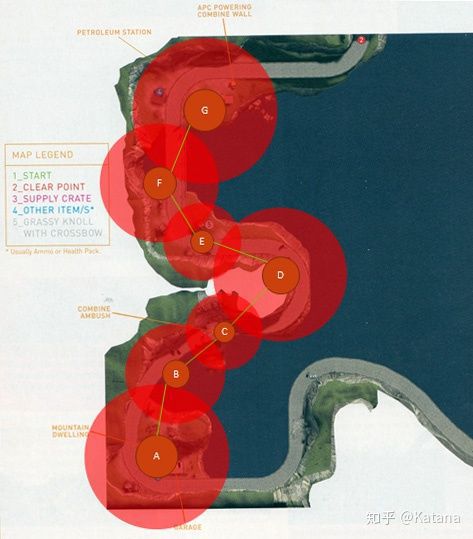
为了更好地去说明“多米诺理论”是如何工作的,让我们使用“半条命2”中的相同例子,但这次我们故意去破坏体验密度(图11)。在图11中,重叠的游戏区域将由重叠的红色AOE所表示。从玩家体验的角度来看,这就像在尝试阅读一本没有任何标点符号的书。用皮诺的话来说,
游戏体验缺乏令人满意的情感融合,因为玩家“除了发现微妙之处以外什么都没有发现”。
图11
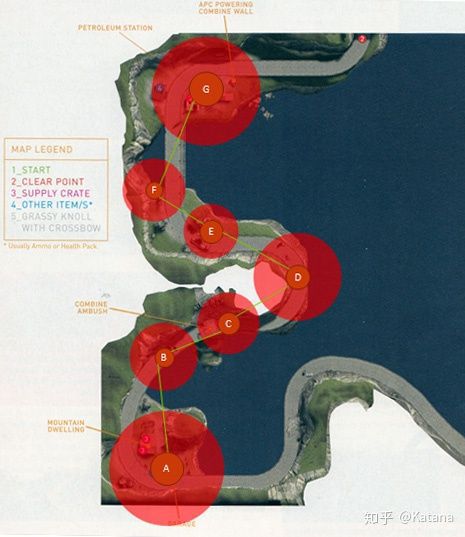
因此,这张地图是应用了多米诺理论来解决体验密度问题的主要候选者。根据你希望玩家所拥有的情感冷却区域的数量,你可以调整“多米诺重叠”的规则以此适应你的设计目标。例如,你可以从元素中删除重叠的节点,以促使它们不会再产生重叠(如图10所示),或者你可以修改你的游戏区域,以促使游戏强度更低而出现的频率会更频繁(如图12所示)。
图12
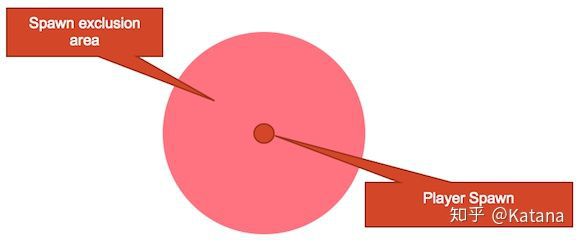
从关卡概念的角度来看,多米诺也可以用来定义“出生点排除区域”或任何其他类型的“排除区域”。
排除区域可以定义一个不应该发生某些事情的区域,即不应该与另一个节点的域重叠。在该多米诺理论的应用中,节点可以表示一个拾取点或者是一个玩家的出生点。因此,红色AOE是空间度量的视觉表示,你可以使用它来表示到发生事件的最小距离。
图13是使用多米诺定义一个排除区域的示例。该节点表示实际的玩家出生点,但也可以是任何的游戏代币。节点周围的红色AOE是另外一种出生点存在可能的最小距离的视觉表示。例如,如果我们在UDK(UE引擎前身的免费版)的限制内工作,那么我们可以说,根据我们地图的大小,如果每个出生点占用着相同的垂直空间,则它们必须至少相距1024UU。
你的多米诺区域的规则是灵活的,但是,对于这个例子来说,规则是在多米诺区域内没有任何其他的出生点——至少从平面图的角度来看。
图13
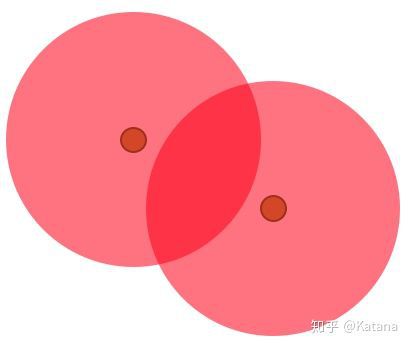
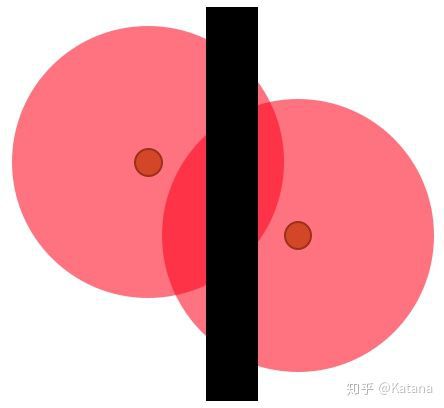
图14是一个需要解决的多米诺问题。该问题可能是由于重叠的出生点或拾取点过于接近所导致。我们可以通过将这些节点进一步的分开,或者简单地使用关卡几何体来减少重叠,从而消除多米诺区域中的重叠,如图15所示。
图14
图15
在具体运用多米诺理论时,运用常识是很重要的。一旦开始去添加关卡几何体,就会在设计中增加另一层的复杂度,这将会要求我们去修改某些规则。
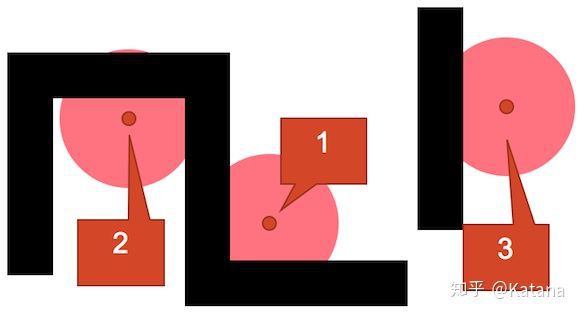
图16
在图16的示例中,我使用了出生点排除系统在非对称环境中分布出生点位置。需要注意的一点是,生成点3被有意地移到离生成点1和2更远的地方。
其原因是由于第1和第2生成物具有较少的接近矢量-即玩家可以在它们的视野中看到任何迎面而来的敌人。
另一方面,出生点3具有一个很宽阔的接近矢量弧,玩家可能无法在同一视锥范围内覆盖它,因此需要通过将其远离其他出生点来进行补偿。
你可以将这个相同的出生点排除系统应用于其他的拾取物-拾取物越强大,则生成物的排除区域就应该越大。
如前面所述,关卡的几何形状和其他因素(例如拾取物分布和玩家在游戏空间内移动的能力)将需要使用更复杂的分析工具-生成树和斯坦纳点。
运用图形理论理解玩家的选择和策略
所有的游戏关卡都提供了某种类型的空间去解决谜题。虽然这些谜题拥有多种形式,但是有一种类型的谜题则是可以通过应用图形理论而加以改进的谜题,那就是与在所有精心设计的死亡竞赛式的地图中,我们看到的
最佳运动策略相关的谜题。
玩家们喜欢选择;然而,
选择太多可能会和选择太少一样糟糕。除此之外,玩家对于
通过去执行“良好”策略的选择获得胜利时会感到非常自豪。到目前为止,我们使用了图形理论来研究游戏空间的构造;但是,当我们以人类的狡猾和策略为主要考量来研究我们的水平设计时,图形理论则尤其表现出了它另外的作用。斯坦纳树、生成树以及最大和最小切割原理都是我们尝试去理解这些人为因素中所不可或缺的理论。
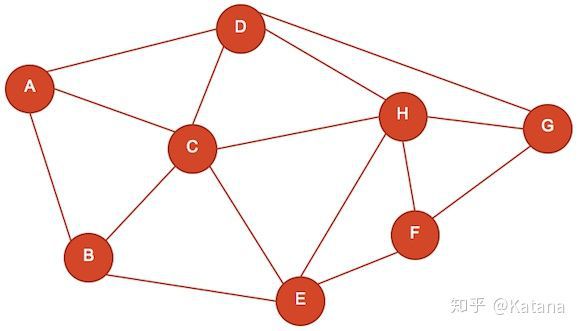
图17
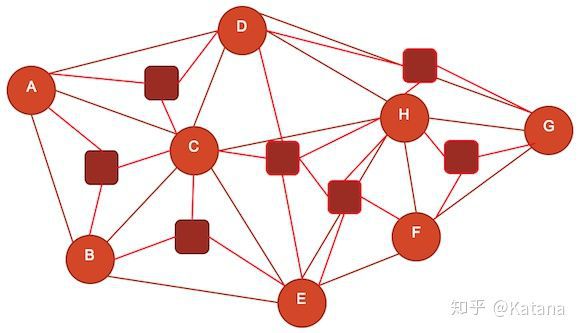
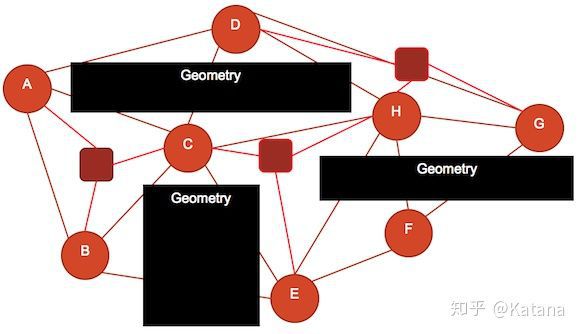
图17是一个假设的关卡示例。每个节点(指定A-H)表示着不同类型的游戏空间,每条边线则用来表示玩家可以从一个空间移动到另一个空间的不同方式。请注意,每条边线并不是代表走廊,而是代表着玩家的选项。边线的长度是短还是长取决于特定路线的复杂程度——
即,边线越长,使用该选项所需的时间以及消耗就越多。在图17中,每个空间(节点)有三到五个不同的选项供玩家在探索空间时考虑。该图还传达了玩家需要如何在空间中移动才能得以遍历整个地图。
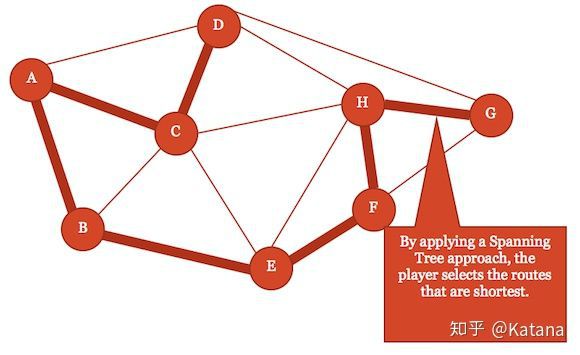
图18
生成树可以用来定义图中节点的最佳连接。当我们试图去理解玩家在地图中的行为并去寻找设计中可能不公平或者是不平衡的方面时,这个工具也很有用。我们可以使用生成树(如图18中所示)来帮助分布拾取物、定义出生点和放置关卡几何体,以帮助抵消PvP地图中可能出现的任何明显的过大优势的(OP)移动策略。
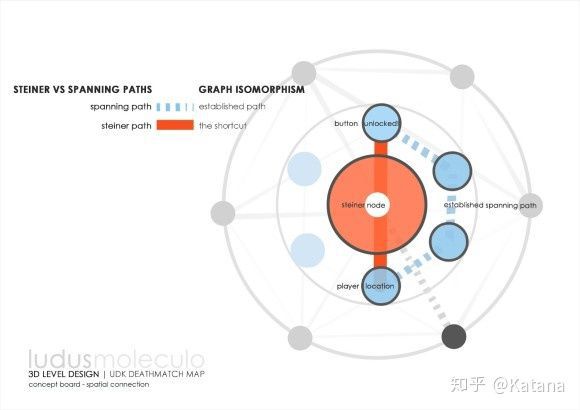
虽然说去
为一个关卡去设计最佳移动策略的特定排列是一个开始明确游戏空间的好方法,但至关重要的是,我们必须进一步的考虑到玩家的狡猾与其一时兴起的欲望。关于这一点的一个很好的例子是考虑到人们(不仅仅是玩家)在识别捷径时的所感受到的自豪感。捷径是超出常规考虑范围的一系列战略选择。玩家在任何的游戏环境中都会想要去寻找这样的机会,他们对于这种机会的发现和利用在情感层面上可能会非常令人满意。而理解这种行为的一个很好的方法则是来自于斯坦纳树理论。
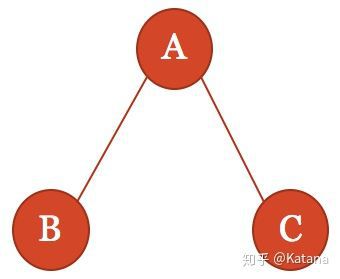
斯坦纳树是一种在多个节点之间寻找最短互连的空间问题。Raph Koster在他的“Games are Math”演示中所给出的示例,是我们尝试理解斯坦纳树在游戏中应用的一个很好的方法。在他的演示中,Koster说:“
如果你有三个节点,并且你需要在它们之间创建最短的可能路径,那么所需的最短边数是多少?”Koster说大多数人会回答类似于图19的问题。
图19
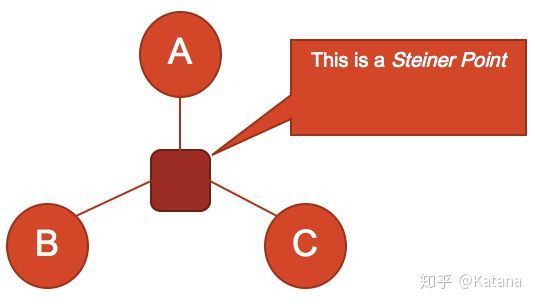
这个问题的答案稍微有点曲折,因为它需要我们在谜题中去添加另一个节点——
斯坦纳点。通过引入图20中的斯坦纳点,我们得以
为这个谜题创建了最为理想的解决方案。斯坦纳点及其创建的边线可以像任何其他类型的图形一样处理。在游戏的上下文中,我们可以使用加权边线和有向边线来帮助定义一个斯坦纳点,它是如何成为地图中的高度元素,或是可作为另外一个单向门,像
传送门或者是
跳板那样。
图20
斯坦纳点是一种捷径。 玩家将主动去寻找关卡设计中的要素以进行二次开发。关卡设计人员的秘诀则是,使地图中的斯坦纳点看起来并不像生成树路线那么明显。 无主之地就是一个非常好的例子。 在地图中,生成树的路径已经被明确的定义了,并且在大多数的情况下,它们是被明确定义的路径和龙门架或(道路的)路标架。
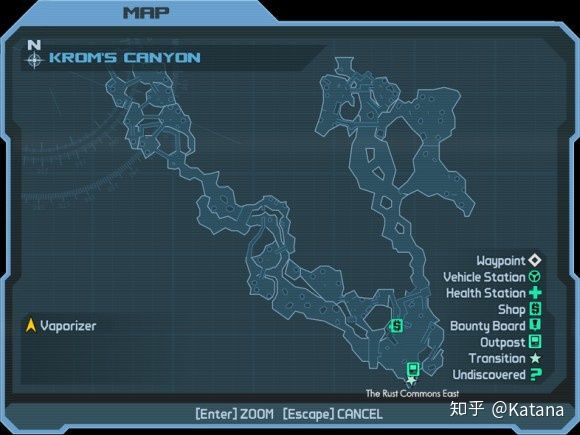
斯坦纳点通常作为高度元素的形式存在于游戏当中,高度元素使玩家可以通过直接跳到地图的某些区域,以此来直接越过生成树的大部分区域,从而使玩家避免了在地图中大范围的遍历找路。无主之地中的克罗姆峡谷(Krom's Canyon)就是一个经典的例子,玩家从高架平台上跳下来,快速移动到地图上的另一个点,这个过程便创建了一个斯坦纳点(见图21)。
图21
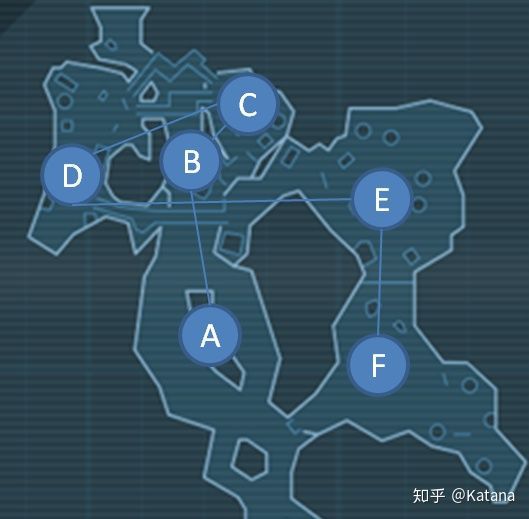
图22(取自上面的克罗姆峡谷)是一个
从关卡设计角度来解释生成树和斯坦纳点如何工作的示例。 在此示例中,为了让玩家从节点A到达节点F,他们必须制定生成树的解决方案。 在关卡设计中,这种关联由一组通过桥梁相互连接正逐渐上升的平台来表示。在地图的这一部分中通过斯坦纳点实现分布了许多的奖励物品。
图22
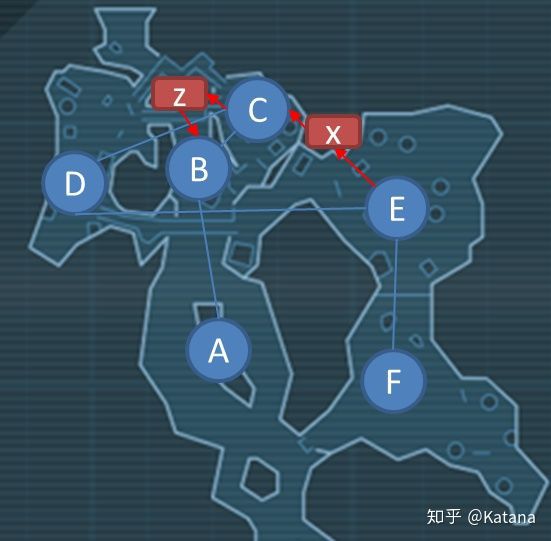
在图23中,添加了两个斯坦纳点。虽然实际上还有其他的一些斯坦纳点存在于这个空间元素里,但这些节点是被放置在高台上的拾取物,玩家只能从它们上面的节点去访问。
因此,这些不仅作为斯坦纳点提供了捷径,而且还为玩家带来了重要的兴趣点,促使他们能够探索环境,将其视为空间谜题,而不仅被认为是斯坦纳点。
图23
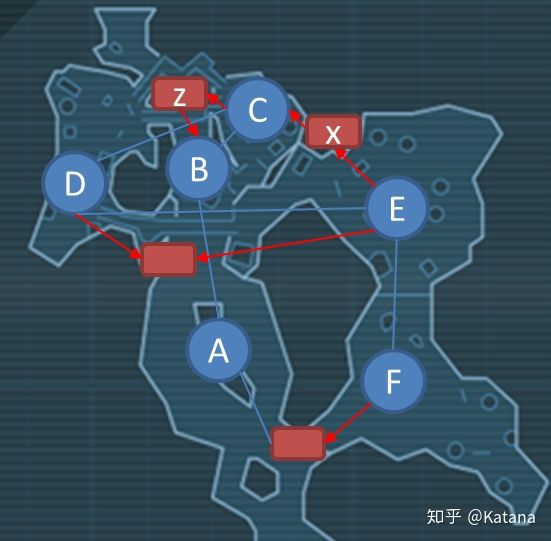
图24将游戏的这一特定部分扩展为一个更为明确的元素,并添加了另外两个主要的斯坦纳节点,这些节点显示了玩家在上升或下降时是如何穿越空间。
图24
现在,我们已经
从空间谜题的角度上研究了斯坦纳点是如何工作的,再来让我们重新回顾一下图17中最初介绍的生成树元素。如果我们将斯坦纳点应用到紧密相邻的链接节点上,那么我们将拥有类似于图25所示的内容。
图25
这些斯坦纳节点可以采用有多种形式。他们可以是传送门,或者是实际的关卡几何体,甚至是允许更快地遍历路径的高度元素。图25展示了在这个空间设计中我们可能具有多少斯坦纳点。据Koster说,太多的斯坦纳点对人类玩家来说是不利的,因为你提供了太多的机会;实际上会导致玩家没有额外的空间,得以去练习被我喜欢称之为“巧妙策略”的东西。基本上,在这种环境中创建捷径不会带来任何的乐趣,因为太多了,它们(指捷径,斯坦纳点)实在是太多了。
图26
如果我们开始使用关卡几何体来减少斯坦纳点的数量,我们将开始
对玩家提出更多的要求。 通过给他们更少的选择(图26),我们会
要求玩家比地图上的其他玩家执行更好的策略。 这样做的好处是,
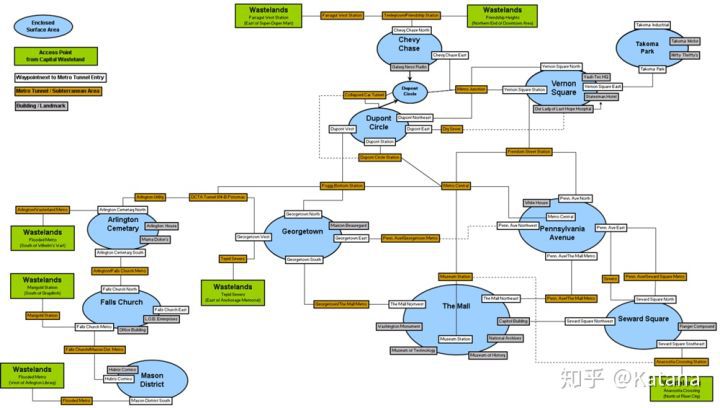
在这种环境中所表现出色的玩家将从成功完成的游戏比赛中获得更大的满足感,因为他们认为自己没有选择时,所遇到的问题将会更加的复杂。为了证明斯坦纳点数量的减少与游戏强度增加之间的关系,我们只需要看看在Fallout 3 Overworld地图东部区域中所看到的斯坦纳树问题(见图27)。
图27
辐射3早期部分的空间导航问题是通过简单的生成树来解决的,在生成树中有很多可能的斯坦纳点。 这一点在主拱顶以南的区域最为明显,因为这是在预期内玩家探索的地图的第一部分(也是最容易的部分)。 但是,
随着游戏强度的不断增加,这些斯坦纳点也会大大减少。 这可以在DC的地铁系统中看到,玩家在稍后的《辐射3》的主线任务中将会遇到。
实际执行
到目前为止,我们已经研究了图形理论的基本原理,并将其应用于一些商业实例的分析,但是
将图形理论作为概念游戏空间的工具是如何堆积起来的呢?下面是Nassib Azar所创建的元素设计理论的一个实际例子。
在本例中,为了创建一个平衡的多人游戏空间,我们对元素的概念进行了测试、实施和完善,尽管它很简单,但是仍然为玩家提供了许多有趣的战略探索的可能性。
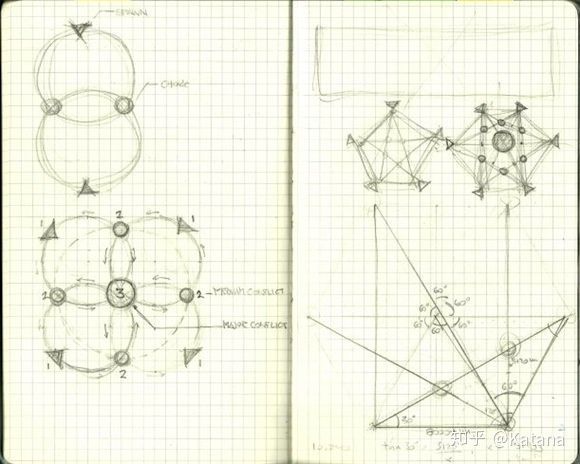
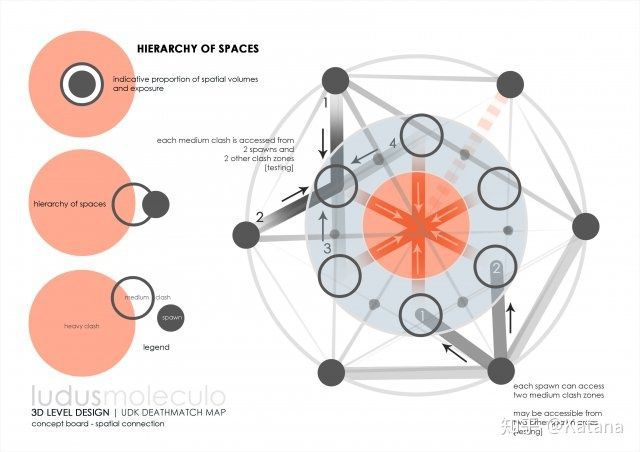
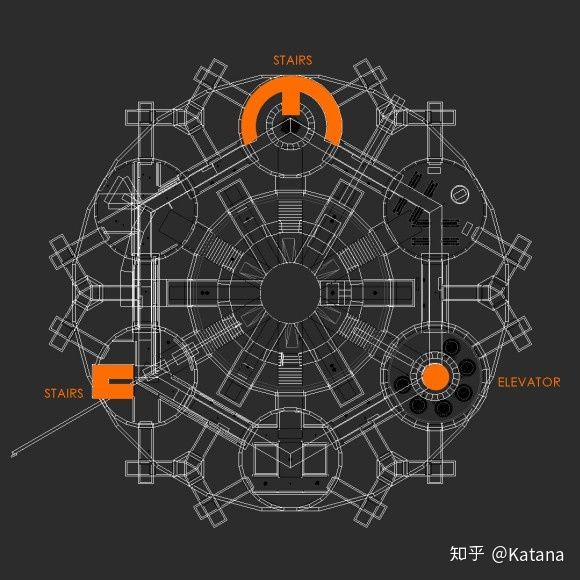
Nassib决定探索的核心思想是一个具有三层游戏体验的地图设计,具体用三个同心圆来表示。游戏空间则是使用UDK的默认游戏类型中的死亡竞赛地图模板。外层由低强度区域所以组成,用于将玩家“喂入”游戏空间的最内部区域。
在这个设计案例中,“强度”是指玩家在每个区域内积极地尝试击杀的敌人数量来衡量的。图28是该地图的预制作草图之一。
这个图探索了当玩家尝试接近地图中心时,应如何使用阻塞点,交叉点,出生点和武器拾取来增加游戏体验的强度。
图28
经过一些最初的纸面原型和反馈后,三个强度不同的同心游戏空间的核心思想最终发展成为一个更具体的元素,整个空间被它定义了出来。图29是早期概念的迭代。在这个迭代中,我们仍然具有相同的一组同心圆,用它们表示游戏的强度;但是,我们增加了边线来描述是如何从外部区域是进去中间区域的。
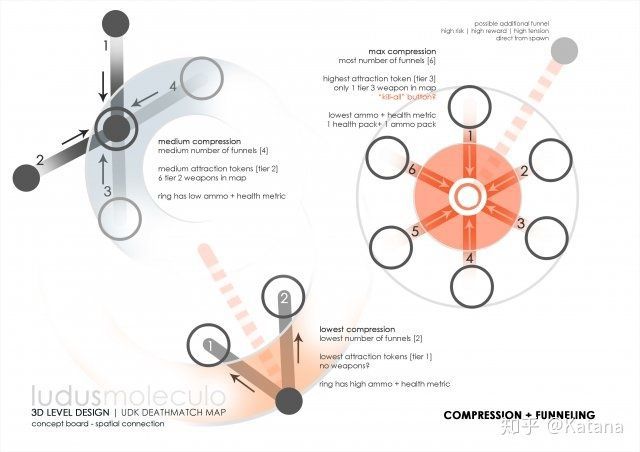
为了实现这一目标,Nassib应用了“压缩和漏斗”的概念,这是一个简单的工具,着眼于如何使用各种游戏元素迫使玩家在游戏空间中徘徊,从而创造出更高的情感体验。在图29中,每个边线代表它们导致的节点上的附加压缩向量。在此示例中,节点表示冲突空间;
进入节点的边线越多,则该节点上的压缩程度就越高(因此,游戏体验的强度就越高)。在这个应用中,节点的大小用来表示所增加的压缩率,以及随后的游戏强度。
图29
尽管元素设计的应用是为了区分游戏体验和关卡几何体,但Nassib选择探索空间的纯粹几何表示是否具有内在的玩家体验价值。Nassib元素原型的六边形的特性值得进一步的研究。真正的问题是:这个元素应不应该转化成实际的关卡几何体,并且仍然保留最初的设计意图?
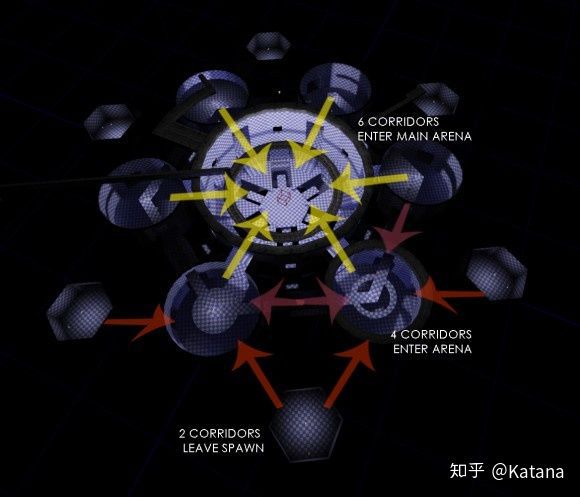
用于定义整个游戏空间的原型元素以UDK内部所开发的灰盒关卡形式经过了多次的迭代。通过原型制作,可以很明显的看出这个实验是有价值的;
玩家体验的强度会随着他们朝着地图中心的方向前进而增加。此时节点变成了一般的游戏空间(房间),边线则变成了可以进入这些空间的走廊。
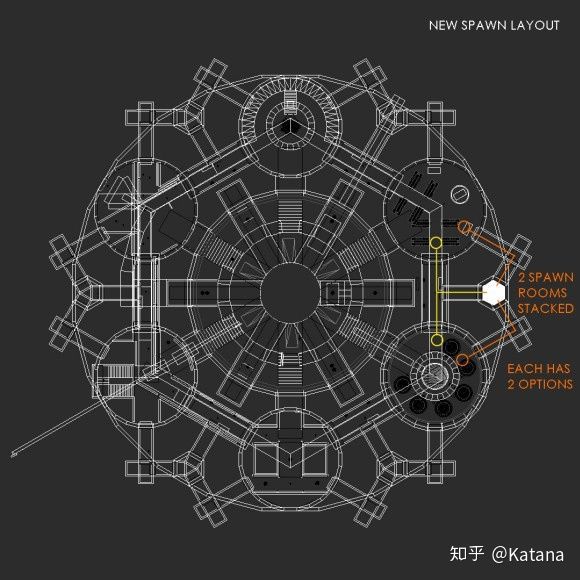
图30是灰盒的更高级迭代之一。它展示了初始元素在可玩空间的实现。在测试过程中,我们发现为了增加游戏强度,需要增加房间的大小以适应和游戏强度的变化。
房间的大小旨在于为了所需的游戏强度,而创建最佳的区域大小。最初的元素设计在这方面转换得很好。随着玩家向地图的中心的移动,游戏区域逐渐变得越来越大,但同时空间又变的足够的小,迫使了玩家接近战斗,从而增加游戏强度。
图30
为了制造一个朝向地图中心的玩家虹吸管(用以输送玩家),我们设计了一个元素来帮助放置各种武器拾取点。有两个主要的元素用来定义标记的位置。武器拾取点嵌入了一个元素,迫使玩家快速向地图中心移动。HP拾取点也嵌入一个元素,迫使玩家探索每个游戏区域的圆形边界。
这两种元素的不同性质,增加了为进攻和防守的比赛制定了明确的界限,以及不同的移动策略。而且还有助于将比赛分散在整个地图上,而不是仅在最中心的区域发生战斗。
图31
图31进一步地分解了图形。在中间节点(左上角)的特写镜头中,对导致它的两个不同边线类型进行了区分。边线1和边线2来自出生点,而边线3和边线4来自其他的中等节点。这意味着危险程度有所不同,因此我们可以通过不同地表示边线来表示。尽管在最初的设计中,我们假设的示例,表明了边线1和边线2以及边线3和边线4之间会存在着某种类型的可分辨的差异。但是我们仍需要对灰盒进行多次修改才足以看到到该假设中的这个真实世界,如图32所示。
图32
灰盒的早期迭代表明了设计中所存在的一个根本缺陷。 尽管游戏在接近到达地图的中心范围时,游戏强度变得越来越激烈,但是却出现了第二个机制。
玩家意识到可以在地图的外圈提前埋伏因此得以捕杀大量刚刚复活的玩家。作为测试的结果,将边线[走廊]1和2升高以创建单向门,通过单向门将玩家送入地图,但不允许地图中已经存在的玩家去访问出生点。如图33所示,高架走廊在物理空间中被重新概念化为检修井(即SHAFT FROM SPAWN处的通道)。
图33
拾取物的放置也得益于元素设计的方法,并遵循了与关卡几何体所相似的对称布局。虽然对称元素的运用为地图设计创造了一个简单的工作流程,
但过多的对称性往往会让玩家感到无聊甚至困惑。
为了解决这个问题,非对称性往往被用于为玩家创建导航作用的地标,以及突出不同类型的武器特点和游戏机制的房间。每个房间布局的差异有两个目的:协助玩家导航并为每个房间创建出“态势感知”上的优势。玩家所感知到的不公平现象则表明,无论系统是多么公平或者平衡,玩家都将会被他们认为已经被破坏的游戏元素所吸引,即使他们没有被破坏。
本质上,第二环范围中的每个房间都包含着不同类型的空间元素。这些元素因阻塞点和重叠元素的不同而不同。其结果可以从图34和图35的比较中看出;两者都是位于第二环的房间,并且都
提供了不同类型的游戏体验。
图34
经过进一步的迭代和测试,我们发现玩家进入主要房间的次数多于进入第二环范围/中环房间的次数,但是仍没有达到预期的比例。中心房间的游戏体验强度必须非常高,然而实际上却根本没有足够的玩家流量来获得预期的体验。当然,这时我们可以通过修改该块的空间使其变的更小来解决此问题。但是,由于许多关卡艺术上的资产已经投入了生产,因此我们
有必要去考虑其他的方案。
为了增强这种体验,我们将创建第二个环形夹层,促使在该环形的夹层上创建出生点。从上层的出生点到中心房间的步行距离比一楼短,
这将鼓励了更多的玩家流量涌进中心房间,因此最终达到了我们预期的效果。
图35
图36中的两个产生重叠的出生点对于其中的房间来说,并没有相同的出生时间和交战时间。换句话来说,上面的边线不等于下面的边线。
通过改变出生点的位置与修正空间元素设计的一致,与现有的出生点相比,交战时间可以忽略不计。
图36
在地图上,对称元素帮助我们创造了楼梯和电梯的合理分布;然而,这三个电梯的实际设计是我们有意改变的(图37)。这种方法的基本原理是
强调了人们认为不公平的心理。经过测试,结果表明大多数玩家认为他们自己的出生点附近的楼梯为他们提供了优势,而这种优势却又并没有被别人用来对付他们自己。楼梯本身的设计也采用了非对称性的设计,这又同时起到了两个作用:辅助导航并改变了中型房间的游戏体验。
图37
另一个用于平衡的策略并不是图形理论本身,而是强调图形理论是如何帮助我们去理解玩家的行为。我们创建了一个Kismet脚本,在该脚本中,游戏每三分钟将比较经过六个中型房间的玩家数量,并确定哪个房间的流量最小。玩家活动次数最少的房间将会生成触发器。
当触发器被玩家按下时,此触发器会将所有的其他玩家发射到太空,杀死他们并为发动者加分。(图38是从地图顶部开始的视图,这是玩家在死之前所见的最后一件事。)这至少鼓励了“热图”的诞生。因此,
动态平衡系统是通过机制而非静态图形所创建的。在这种情况下,玩家可以选择使用斯坦纳点解决方案来解决空间问题-即到达目标的最短路径是什么。
图38
一旦脚本确定了流量最小的房间,地图上的所有玩家都将会收到对应的声音和控制台通知,让他们知道脚本触发器被作用于哪个中型房间。
根据玩家当前的位置,他们将面对两个主要的选择。他们可以使用危险但最短的路径穿过中心,但也可以通过较长但更为安全的路径穿过中型房间,从而避开中央的冲突区域(冲突交战区域可参考该系列的另外一篇文章来了解)。
通过这样做,我们为玩家创建了两种截然不同的策略;他们可以将中间的房间作为斯坦纳节点,或者是使用外部的房间作为生成树的解决方案(图39)。这些战略选择对玩家的成就感将会起到不同的作用。玩家会有一种自豪感,因为他们觉得走捷径到合适的房间比其他人都聪明。用于填充各个房间的关卡资产还可以
减少潜在可能的斯坦纳点的总数量,为找到有限的解决方案之一从而创造了更高的内在价值。
图39
最终公布的地图经过了8次大的迭代修改,结果要么是更新了灰盒,要么便是更新了元素本身,从而获得了最终的产品。每次修改的基础是一个修正后的元素概念,我们将其转换成一个灰盒。
因此,每一次的迭代修改都具有着明确的目的和目标,并且由于时间极其有限,最终产品往往能够从中受益匪浅。
结论
像丹·库克(Dan Cook)和克里斯·克劳福德(Chris Crawford)这样的人正在研究人们玩游戏的动机,他们认为其动机根本原因起源于我们通过去学习和证明这些新获得的技能的需要。拉夫·科斯特(Raph Koster)则通过更加具体地方式阐述了这一观点,他认为人们是图形识别的机器,当我们在识别图形并抢占它们时,我们会从游戏中获得乐趣。因此,有理由认为,使用基于图形的元素设计方法来定义游戏空间,将可以很快满足这种需求。
并且有一个需要考虑的主要因素是:
玩家并不会将游戏视作为一个平面的地图;他们是从自己所操控的镜头视锥来感知地图和空间的。因此,想要实现的元素规模和“可识别性”,在很大程度上将会受到玩家在游戏中任何一个位置上,所能感受到的游戏世界的限制。
设计师经常会创建迷宫式的地图,虽然从平面的角度上很容易理解,但是从玩家有限的角度来看,这些地图是绝对不可能所跨越的。
因此,元素和他们所创造的图案不一定会是非常复杂的,这样才能够使它们成为玩家的“乐趣”。
相反,取而代之的则是,精心设计的游戏空间往往具有许多嵌套的元素,而不是将空间定义为一个整体的元素。从图形的角度来看,Nassib Azar创建的实际示例可能相对简单,但是由动态的游戏元素所创建的元素排列的数量则为玩家创建了一组富有多样性的、可管理的策略供他们去探索。
重要的是要指出,运用图形理论对游戏空间进行概念化和分析不是一个新的概念,而是一个已经被不同的作者以不同形式所进行讨论过的想法。这项研究的最初灵感来自Raph Koster,他的游戏是Math演示,我将向任何对理性设计方法感兴趣的人推荐Koster的演讲。 Joris Dormans也有一些内容丰富的文章,涉及图形理论以及如何成为关卡设计师的强大工具。 Dormans在关卡设计和作为模型转换的关卡设计中的冒险[链接]则非常出色,并且
展示了了此工具集的丰富的可延展和可塑性。
原作者:Luke McMillan,Nassib Azar
文章原链接:https://www.gamasutra.com/view/feature/184783/the_metrics_of_space_molecule_.php?print=1
作者:Katana编译
专栏地址:https://zhuanlan.zhihu.com/p/100772793