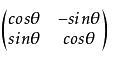More
GameRes游资网在以下平台有媒体号，欢迎关注收藏：

微信公众号

微博 

头条号

百家号

网易号

知乎号

从零开始做一个SLG游戏（三）：用unity绘制图形

作者：观复 2019-10-11

本文主要是使用mesh制作一些简单的模型资源。

一般而言，模型的制作最好还是使用专业的软件来做，但是制作一些简单的模型，unity还是可以胜任的。

unity自带的模型只有立方体，圆柱，球，胶囊，方块等有限的几个，所以稍微复杂一些的东西就不好做了，比如最常用到的圆锥，棱柱，棱台等，十分困难。

所以首先要做的是，将一些常用的基本模型，实现出来。

首先要做的是写一个模型基类:

  1. using System.Collections;
  2. using System.Collections.Generic;
  3. using UnityEngine;
  4. [RequireComponent(typeof(MeshFilter), typeof(MeshRenderer), typeof(MeshCollider))]
  5. public abstract class BasePoly : MonoBehaviour {
  6.         Mesh mesh;
  7.         private List<Vector3> vertices;
  8.         private List<int> triangles;
  9.         private List<Vector2> uvs;
  10.         private float length = 100f;
  11.         private void Awake()
  12.         {
  13.                 mesh = GetComponent<MeshCollider>().sharedMesh = GetComponent<MeshFilter>().mesh = new Mesh();
  14.                 mesh.name = "PolyMesh";
  15.                 vertices = new List<Vector3>();
  16.                 triangles = new List<int>();
  17.                 uvs = new List<Vector2>();
  18.         }
  19.        
  20.         // Update is called once per frame
  21.         void Update ()
  22.         {
  23.                 DrawMesh();
  24.         }
  25.         private void DrawMesh()
  26.         {
  27.                 Clear();
  28.                 Draw();
  29.                 UpdateMesh();
  30.         }
  31.         protected void AddTriangle(Vector3 v1, Vector3 v2, Vector3 v3)
  32.         {
  33.                 AddConer(v1);
  34.                 AddConer(v2);
  35.                 AddConer(v3);
  36.         }

  38.         protected void AddSquare(Vector3 v1, Vector3 v2, Vector3 v3, Vector3 v4)
  39.         {
  40.                 AddTriangle(v1, v3, v2);
  41.                 AddTriangle(v2, v3, v4);
  42.         }

  44.         private void AddConer(Vector3 point)
  45.         {
  46.                 int count = vertices.Count;
  47.                 vertices.Add(point);
  48.                 triangles.Add(count);
  49.                 uvs.Add(new Vector2(point.x / (2 * length), point.z / (2 * length)));
  50.         }

  52.         private void UpdateMesh()
  53.         {
  54.                 mesh.vertices = vertices.ToArray();
  55.                 mesh.triangles = triangles.ToArray();
  56.                 mesh.uv = uvs.ToArray();
  57.                 mesh.RecalculateNormals();
  58.                 mesh.RecalculateBounds();
  59.         }

  61.         private void Clear()
  62.         {
  63.                 mesh.Clear();
  64.                 vertices.Clear();
  65.                 triangles.Clear();
  66.                 uvs.Clear();
  67.         }

  69.         public virtual void Draw()
  70.         {

  72.         }
  73. }
复制代码


具体实现的原理，在上一篇文章里大部分都有讲过。现在将之封装了起来。

在子类中，重写Draw()函数，调用下面两个函数即可绘制各种想要的图形。

AddTriangle(Vector3v1,Vector3 v2,Vector3 v3);

AddSquare(Vector3 v1,Vector3 v2,Vector3 v3,Vector3 v4);

首先实现一下正多边形：


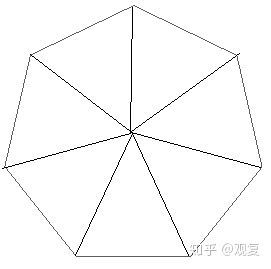
正多边形其实和前面六边形的制作方式类似，不过我们需要手动计算出正多边形的各个顶点。

将正n边形的各个顶点和中心点连线，可以得到n个等腰三角形，而等腰三角形顶角的大小为(360°/n)。

所以，如果知道一个顶点p的坐标，同时又知道原点坐标(0,0)的话，那下一个顶点p'的坐标可以通过p围绕原点旋转(360°/n)的角度获得。

那么我们复习一下高中的空间几何知识：

一个点围绕原点逆时针旋转θ角的时候，我们可以通过旋转变换来获得旋转后的坐标。

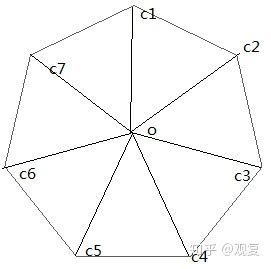
旋转变换的矩阵为：


具体用法为：

对于(x,y)进行旋转变换后，得到的(x',y')有

x'=x*cosθ-y*sinθ

y'=x*sinθ+y*cosθ

所以写一个函数来实现旋转变换：

  1. Vector3 RotationTranslate(Vector3 pos,float angle)

  3.         {

  5.                 Vector3 Pos = pos;

  7.                 float[,] transRect = {

  9.                         { Mathf.Cos(angle),-Mathf.Sin(angle)},

  11.                         { Mathf.Sin(angle),Mathf.Cos(angle)},

  13.                 };

  15.                 Pos.x = pos.x * transRect[0, 0] + pos.z * transRect[0, 1];

  17.                 Pos.z = pos.x * transRect[1, 0] + pos.z * transRect[1, 1];

  19.                 return Pos;

  21.         }
复制代码

angle为旋转的角度。

正多边形的各个点都有了，然后通过画三角的方式，将正多边形画出来了。

代码如下：

  1. public class Polygon : BasePoly {
  2.         public int edgeCount = 3;
  3.         private float angle = 0f;

  5.         private List<Vector3> coners = new List<Vector3>();

  7.         public override void Draw()
  8.         {
  9.                 angle = 2f * Mathf.PI / count;
  10.                 Vector3 pos = new Vector3(1f, 0f, 0f);
  11.                 coners.Add(pos);
  12.                 for (int i = 0; i < count; i++)
  13.                 {
  14.                         pos = RotationTranslate(pos);
  15.                         coners.Add(pos);
  16.                 }
  17.                 for (int j = 0; j < count; j++)
  18.                 {
  19.                         AddTriangle(coners[j], Vector3.zero, coners[j + 1]);
  20.                 }
  21.                 coners.Clear();
  22.         }
  23.         Vector3 RotationTranslate(Vector3 pos)
  24.         {
  25.                 Vector3 Pos = pos;
  26.                 float[,] transRect = {
  27.                         { Mathf.Cos(angle),-Mathf.Sin(angle)},
  28.                         { Mathf.Sin(angle),Mathf.Cos(angle)},
  29.                 };
  30.                 Pos.x = pos.x * transRect[0, 0] + pos.z * transRect[0, 1];
  31.                 Pos.z = pos.x * transRect[1, 0] + pos.z * transRect[1, 1];
  32.                 return Pos;
  33.         }
  34. }
复制代码

实现后，会发现一个问题，那就是每帧都要绘制一次，会非常消耗功能，所以我们需要加一个函数，用于判断是否需要再绘制一遍：

  1. using System.Collections;
  2. using System.Collections.Generic;
  3. using UnityEngine;
  4. [RequireComponent(typeof(MeshFilter), typeof(MeshRenderer), typeof(MeshCollider))]
  5. public abstract class BasePoly : MonoBehaviour {
  6. ……
  7.         private void DrawMesh()
  8.         {
  9.                 if (NeedDraw())
  10.                 {
  11.                         Clear();
  12.                         Draw();
  13.                         UpdateMesh();
  14.                 }
  15.         }
  16.         public virtual bool NeedDraw()
  17.         {
  18.                 return true;
  19.         }
  20. ……
  21. }
复制代码

然后再在子类中重写NeedDraw()函数：

  1. public class Polygon : BasePoly {
  2.         public int edgeCount = 3;
  3.         private int count = 0;
  4.         private float angle = 0f;

  6.         ……
  7.         public override bool NeedDraw()
  8.         {
  9.                 if (edgeCount == count)
  10.                 {
  11.                         return false;
  12.                 }
  13.                 else if (edgeCount < 3)
  14.                 {
  15.                         return false;
  16.                 }
  17.                 else
  18.                 {
  19.                         count = edgeCount;
  20.                         angle = 2f * Mathf.PI / count;
  21.                         return true;
  22.                 }
  23.         }

  25.         public override void Draw()
  26.         {
  27.                 //angle = 2f * Mathf.PI / count;
  28.                 ……
  29.         }
  30.         ……
  31. }
复制代码

其他图形也可以通过类似的方法，一一绘制出来，并通过自己的赋值进行微调。

比较麻烦的一点是，这么实现，需要先让工程运行起来，绘制的图形才能显示出来。幸运的是，这并不影响搭建场景。

接下来将介绍更多的基本图形的画法：

1.正棱锥

棱锥的画法其实和前文制作六边形网格的制作方法类似，将六边形网格的中心点往上移动若干个单位，再加上底面，就是一个六棱锥了。

处理方式和前文的正多边形相同：按角度一次分割三角形


  1. List<Vector3> conors = new List<Vector3>();
  2.         public override void Draw()
  3.         {
  4.                 Vector3 pos = new Vector3(1f, 0f, 0f);
  5.                 conors.Add(pos);
  6.                 for (int i = 0; i < count; i++)
  7.                 {
  8.                         pos = RotationTranslate(pos);
  9.                         conors.Add(pos);
  10.                 }
  11.          }
复制代码


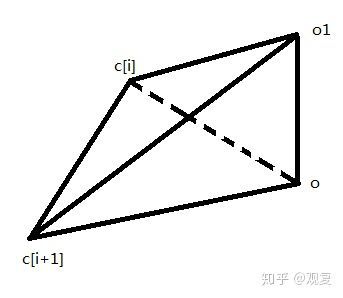
和多边形一样，先把点加进去，接下来和多边形不同的是，我们需要画2个三角形，如下图：


o为底面的中心点，o1为顶点，和前文一样，底面中心的坐标默认为（0,0,0），即Vector3.zero。

o1作为顶点，暂定高为1。于是o1的坐标为(0,1,0)。(0,1,0)也可以表示为Vector3.up。

需要画的三角形为底面的一部分(o,c<i>,c[i+1])以及侧面(o1,c[i+1],c<i>)。

完整代码如下：

  1. List<Vector3> conors = new List<Vector3>();
  2.         public override void Draw()
  3.         {
  4.                 Vector3 pos = new Vector3(1f, 0f, 0f);
  5.                 conors.Add(pos);
  6.                 for (int i = 0; i < count; i++)
  7.                 {
  8.                         pos = RotationTranslate(pos);
  9.                         conors.Add(pos);
  10.                 }
  11.                 for (int k = 0; k < count; k++)
  12.                 {
  13.                         AddTriangle(Vector3.zero, conors[k], conors[k + 1]);
  14.                         AddTriangle(conors[k], Vector3.up, conors[k + 1]);
  15.                 }
  16.                 conors.Clear();
  17.         }
复制代码

2.正棱台

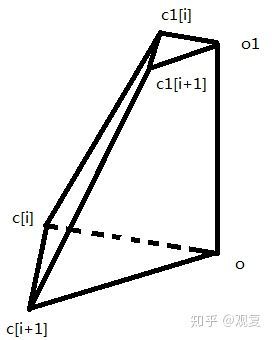
正棱台和正棱锥一样，也是分割成多个方向，单个方向如图：


需要画的是(o1,c1[i+1],c1<i>)(o,c<i>,c[i+1])两个三角形底，以及(c<i>,c[1+1],c1<i>,c1[i+1])这个矩形的侧面。

上下两个三角形的底是相似的，并且对应的边也是相互平行的。

o点坐标为Vector3.zero，即(0,0,0)，o1的坐标为Vector3.up,即(0,1,0)。

然后定义两个三角形的缩放比例为zoom的话

通过空间向量的换算，很容易得出：c1<i>=c<i>*zoom+Vector3.up

所以我们定义两个List用于存放上下底的点，并用一个函数来添加点：

  1. List<Vector3> conors = new List<Vector3>();//下底的点
  2.         List<Vector3> _conors = new List<Vector3>();//上底的点
  3.         public float zoom = 1f;
  4.         void AddConors(Vector3 pos)
  5.         {
  6.                 conors.Add(pos);
  7.                 _conors.Add(pos * zoom + Vector3.up);
  8.         }
复制代码


接下来的就很简单了，点加好后，把三个面加上去就行了，函数都封装好了的：

  1. public override void Draw()
  2.         {
  3.                 angle = 2f * Mathf.PI / count;
  4.                 Vector3 pos = new Vector3(1f, 0f, 0f);
  5.                 AddConors(pos);
  6.                 for (int i = 0; i < count; i++)
  7.                 {
  8.                         pos = RotationTranslate(pos);
  9.                         AddConors(pos);
  10.                 }
  11.                 for (int k = 0; k < count; k++)
  12.                 {
  13.                         AddTriangle(Vector3.zero, conors[k], conors[k + 1]);
  14.                         AddTriangle(_conors[k], Vector3.up, _conors[k + 1]);
  15.                         AddSquare(conors[k], conors[k + 1], _conors[k], _conors[k + 1]);
  16.                 }

  18.                 conors.Clear();
  19.                 _conors.Clear();
  20.         }
复制代码

有了自制的棱台、棱柱，以及unity自带的方块，球，胶囊，圆柱之类的物体，就可以在unity中自己搭建各种需要的场景了。

这样做出来的场景物体，用于最终成品可能不达标，但是用于演示已经够了。这最重要的是，暂时不用去学建模软件了。


相关阅读:

从零开始做一个SLG游戏（一）：六边形网格
从零开始做一个SLG游戏（二）：用mesh实现简单的地形

作者：观复
专栏地址：https://zhuanlan.zhihu.com/p/44918148

最新评论
暂无评论
参与评论

推广
开测游戏 查看更多
决胜巅峰(官服)-预下载 电竞
上线
研发 : 沐瞳   
龙之谷世界 卡通
上线
研发 : 盛趣游戏   
斗笠江湖 武侠
上线
研发 : 上海零酷网络科技有限公司    发行 : 星辰游戏工作室   
沙石镇时光-开放世界沙漠种田 种田
限量删测
研发 : 重庆帕斯亚科技有限公司    发行 : 良心工作室   
仙剑世界-开放大世界 冒险
上线
研发 : 中手游   
水晶传说 回合
公测
研发 : 广州金科文化科技有限公司   
商务合作 查看更多
点点传说
维斯塔的餐桌
星烬 烛耀山海
尸海求生
编辑推荐 查看更多
问剑长生
燕云十六声
纪念碑谷3
星痕共鸣

微信公众号

微博 

头条号

投稿邮箱：news@gameres.com
产品、开测信息邮箱：cp@gameres.com
© 2001-2022 GameRes游资网