非酋的福音？谈一谈游戏内的伪随机机制以及实现

情景一：FGO，新出了一个5%的概率可以抽取saber的卡池，玩家进行踊跃地抽取，如果采用完全的真随机机制，那么会出现哪些情况？

欧洲玩家A：抽取10次以内成功就获得了saber，心满意足
较欧玩家B：抽取11-20次成功获得了saber
较非玩家C：抽取21-30次成功获得saber
非洲玩家D：抽取31-40次才获得saber
非洲酋长E：抽取41-80次才获得saber

那么我们来统计一下，在这次卡池获得中，各种族玩家的人数假设100个人抽，各抽1次，因为为概率为5%，那么5个人第一次便抽中，其余95人抽，同样5%，那么95*0.05的人，抽中，以此类推

玩家A 数量 = 0.05+0.0475+….+0.031512  = 40.13%
玩家B 数量 = 0.029+0.02844+…+0.018868 = 24.02 %
玩家C 数量 = 0.017924+…+0.11297       = 14.38 %
玩家D数量 = 0.010732+…+0.00405       = 8.61%
玩家E数量 = 0.03847+…+0.000312       = 11.1 %

我们将此套数据运用在一个10万玩家投入到了这个活动中的游戏上，会出现怎么样的灾难般的场景？

在

4万人的欧洲玩家A欢呼雀跃，
2.4万的欧洲延边玩家B心满意足，
1.4万的非洲延边玩家C强颜欢笑，
近8600名非洲内陆玩家D失声啜泣，
以及1.1万名非洲酋长玩家E的欲哭无泪中，
“圆满”地结束了此次FGO卡池活动！

实际的运营与开发商，在同等概率的情况下，并不希望有如此极端而真实的概率情况，那么伪随机的机制应运而生，同时削减欧洲人和非洲人数量，各种族人数向玩家B和C之间，靠拢，是普遍目前营运商和开发商的普遍做法，那么如何使用伪随机机制，才能保证，概率的可控性呢？

数值是解决思路的体现：

希望玩家开始抽的时候，抽到概率较低，每抽一次，如果不中，下一次的概率更高，抽到后，概率回归初始值，总体概率与期望相同。重要的是，这个初始值和这个每次概率的累加值，如何确定？才能保证我们的数值的可靠和可验证性。

伪随机模型：等差叠加模型

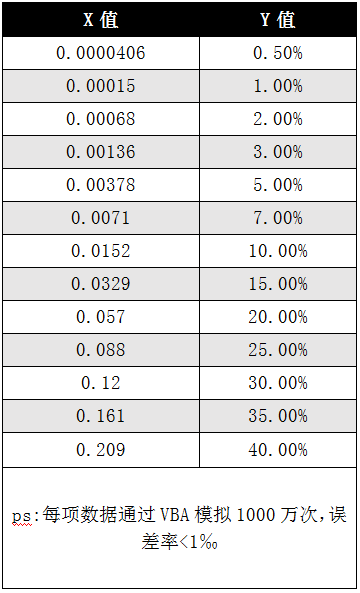
即第一次概率为X，第二次概率为2X，第三次概率为3X….以此类推，最终总体概率为Y确定Y和X，Y为设定的值，假设 Y = 5% ，预估 X的值 ，并将其带入VBA模拟


可得下表


按照该套计算方法下，我们再次计算情景一中玩家数量，即Y=5%，X=0.00378时

假设10000个人抽，各抽1次，因为为概率约为0.38%，即，38人第一次便抽中，其余9962人开始抽第二次，这次概率为第一次的2倍，即0.76%，以此类推

玩家A 数量 = 19.00% (<10次)
玩家B 数量 = 36.74% (11至20次)
玩家C 数量 = 28.21%（21至30次）
玩家D 数量 = 12.25%（31至40次）
玩家E 数量 = 0.037%（41至80次）

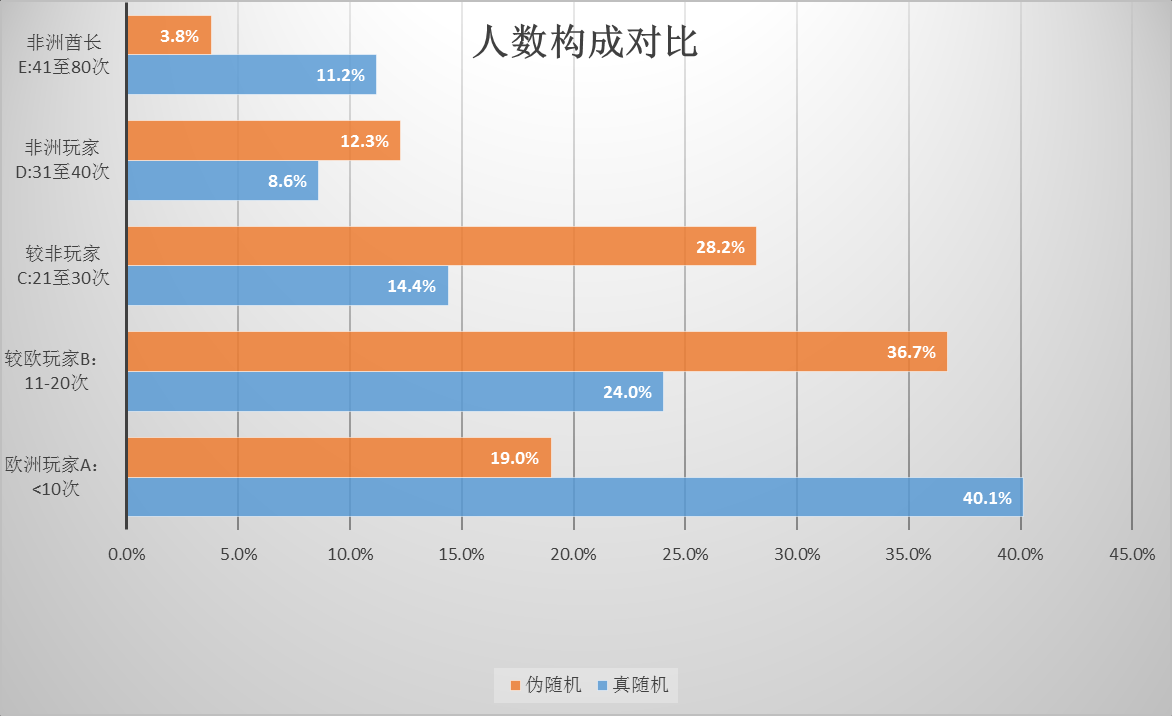
我们看下两种的对比图


由此可见，较真随机的机制来比，采用此套伪随机下，对于玩家体验有如下提升：

1>体验最差的D和E类玩家总数降低，体验最差的E类玩家数量减少了66%
2>总体人数向平均的B和C类玩家靠拢，‘公平性’的感官体验相对于真随机来说，有了很大提升