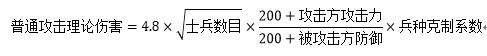浅析率土之滨中的伤害公式和兵种加成对玩家阵容的影响

2017-06-01

hj.tang@outlook.com

我们首先使用控制变量法推导出率土之滨的伤害计算公式，再讨论了这个伤害公式对于玩家体验和战斗回合数的影响。最后讨论了在这个伤害公式下同兵种加成系数对于玩家兵种搭配策略的影响。

1.伤害公式

率土中的伤害分为普通攻击和计谋两类。首先看普通攻击，其伤害与士兵数目、双方攻防属性与部队种类有关。普攻造成的实际伤害会是理论伤害上下5%的范围内的随机值，目前尚不清楚该随机值是否为均匀分布。

接下来是计谋的伤害，与士兵数目、双方谋略属性、部队种类和具体技能有关。

1.1.伤害公式影响

上述的伤害公式分为物理和法术两类属性，与属性的关系是加固定值然后相除。这都是非常常见并且沿用已久的设定，在此不再分析。

值得注意的有以下几点：

a.由于物理伤害有2个属性而计谋只有1个，因此提升相同属性值的情况下，升级谋略相比于升级攻防能够带来两倍的战斗力加成。

举个例子，对于满红武将来说，50点属性可以提高11%-13%的物理攻击或者物理防御，或者提高11%-13%的计谋伤害和计谋防御。

b.克制关系不会放大伤害，只会减少受到的伤害。

这个设定小幅度的延长了回合数，减少速度占优的土豪玩家对平民玩家的碾压程度。

c.伤害正比于兵力的0.5次方，因此战斗力正比于兵力的1.5次方，而不是常见的1次方或者平方。

这样的做法主要有两个原因。第一是这在兵力升级幅度随等级递增的前提下，让进度稍稍落后的玩家相对于进度靠前的玩家有更强的相对战斗力，实际上也是加强了平民玩家。第二是在计谋伤害率增加的前提下保持回合数平缓增长，不至于过快结束战斗。

我们可以看看这个模型下兵力数目对战斗回合数的影响。从1级到满级，武将技能数量从1个增加到3个，技能伤害率一般是会提升到初始伤害率的200%。因此我们可以做出如下一个粗略的估计。

兵力数	1000	2000	5000	10000	20000
标准伤害	152	215	339	480	679
总输出效率（普攻+技能）	1.5	2	3	4	5
期望回合数	4.4	4.7	4.9	5.2	5.9

需要注意的一点是，菜刀队和计策队之间的战斗能够很快分出胜负，因为通常不会增加太多对位的防御属性。但是菜刀队和菜刀队以及计策队和计策队之间的战斗回合数目较长。

d.在升级兵营能够快速提升带兵数量上限的阶段的伤害公式并没有做额外的调整。

我对率土的资源和成长曲线了解的并不是非常清楚，因此也无法判断该阶段是否需要额外调整。不过很大概率上调整这一阶段的伤害公式可以提升体验。

2.同兵种加成系数对兵种搭配的影响

通常来说在这种循环克制的设定下，混合兵种的阵容比单一兵种的阵容有更强的平均战斗力。但是率土中一支部队有两种或者三种相同类型的部队可以获得5%或者10%的属性加成。我们很好奇这样的设定会对玩家的兵种搭配造成什么样的影响。

接下来我们首先求出没有加成的情况下处于纳什平衡的玩家策略，再求出有加成的情况下的玩家策略，最后将它们进行比较。

2.1.计算方式

因为每个位置都有3个不同的兵种选择（此处仅考虑基础类型兵种），所以一共有27种不同的兵种搭配策略。我们计算了这27个不同阵容之间两两对战的结果并找到了最佳策略。

战斗中的一些规则设定如下：

假设每个位置的武将都拥有相同的攻防属性，并且兵力相同，兵种都为初级兵种。
此处采用简化的战斗规则，双方同时出手。由于游戏中攻击目标的选定具有一定的随机性，因此分别采用下述两种规则进行计算。
攻击规则1：双方仅由第一位武将相互攻击至一方死亡，然后由失败方第二位武将接替死亡武将，直至一方三名武将全部阵亡。在本规则中不能体现出射程差异。
攻击规则2：双方武将都优先攻击与自己位置相同的对手，如敌方对应位置武将死亡则攻击位置靠近自己且靠前的对手。
战斗结果的定义：我们将胜利方剩余兵力占初始兵力的百分比定义为战斗结果。胜利为正，失败则为负。

2.2.攻击规则1下无同兵种加成时的最佳策略对战结果

根据对称性易知处于纳什平衡的策略一定是有相同概率使用骑、步、弓的混合策略，因此我们可以用（骑，骑，骑）表示一个有相同概率使用（（骑，骑，骑），（步，步，步），（弓，弓，弓））的混合策略。

由上述规则得到的计算结果如下。

	骑,骑,骑	骑,骑,步	骑,骑,弓	骑,步,骑	骑,步,步	骑,步,弓	骑,弓,骑	骑,弓,步	骑,弓,弓
骑,骑,骑	0.000	0.011	0.038	0.047	0.048	0.094	0.041	0.084	0.021
骑,骑,步	-0.011	0.000	-0.028	0.072	-0.008	0.067	-0.007	0.036	0.025
骑,骑,弓	-0.038	0.028	0.000	0.038	0.002	0.000	0.022	0.061	0.054
骑,步,骑	-0.047	-0.072	-0.038	0.000	-0.038	0.021	-0.021	0.010	-0.057
骑,步,步	-0.048	0.008	-0.002	0.038	0.000	0.017	0.000	-0.023	-0.001
骑,步,弓	-0.094	-0.067	0.000	-0.021	-0.017	0.000	0.041	0.033	-0.029
骑,弓,骑	-0.041	0.007	-0.022	0.021	0.000	-0.041	0.000	-0.022	-0.016
骑,弓,步	-0.084	-0.036	-0.061	-0.010	0.023	-0.033	0.022	0.000	-0.038
骑,弓,弓	-0.021	-0.025	-0.054	0.057	0.001	0.029	0.016	0.038	0.000

最佳策略

简单分析可知纳什平衡为每名玩家皆使用如下的混合策略：

使用(骑步骑，步弓步，弓骑弓，骑弓骑，步骑步，弓步弓，骑弓步，步骑弓，弓步骑)的概率分别为(14%,14%,14%,6.3%,6.3%,6.3%,13%,13%,13%)。

相对于使用该混合策略的玩家，使用其他任何一种单一策略的玩家的收益如下：

策略	骑,骑,骑	骑,骑,步	骑,骑,弓	骑,步,骑	骑,步,步	骑,步,弓	骑,弓,骑	骑,弓,步	骑,弓,弓
收益	-0.06	-0.043	-0.044	0	-0.007	-0.012	0	0	-0.042

可以发现使用3个相同兵种的策略相对于最佳策略有6%左右的劣势。

2.3.攻击规则1下有同兵种加成时的最佳策略

首先我们需要计算出属性加成等效的战斗力加成。因为伤害正比于（200+攻击力），有效血量正比于（200+防御）或者（200+谋略），而这几个数值通常都在100-250的范围内。因此每1%攻击或者血量加成近似于0.3%-0.5%的战斗力加成，而1%的速度我们折算为0.2%的战斗力加成。

实际上2个相同兵种加成数值为5%，3个为10%。加成的属性分别为（攻击，速度），（攻击，防御），（防御，速度）。由此我们可以认为上述两种加成分别提高了3%和6%的战斗力。

对战结果如下。

	骑,骑,骑	骑,骑,步	骑,骑,弓	骑,步,骑	骑,步,步	骑,步,弓	骑,弓,骑	骑,弓,步	骑,弓,弓
骑,骑,骑	0.000	-0.039	0.003	-0.070	-0.014	-0.099	0.011	-0.058	-0.020
骑,骑,步	0.039	0.000	-0.029	0.074	-0.008	0.025	-0.008	-0.001	0.026
骑,骑,弓	-0.003	0.029	0.000	0.039	0.002	-0.049	0.023	0.021	0.055
骑,步,骑	0.070	-0.074	-0.039	0.000	-0.039	-0.101	-0.021	-0.084	-0.059
骑,步,步	0.014	0.008	-0.002	0.039	0.000	-0.051	0.039	-0.077	0.018
骑,步,弓	0.099	-0.025	0.049	0.101	0.051	0.000	0.097	0.033	0.083
骑,弓,骑	-0.011	0.008	-0.023	0.021	-0.039	-0.097	0.000	-0.060	-0.016
骑,弓,步	0.058	0.001	-0.021	0.084	0.077	-0.033	0.060	0.000	0.000
骑,弓,弓	0.020	-0.026	-0.055	0.059	-0.018	-0.083	0.016	0.000	0.000

最佳策略

简单分析可知纳什平衡为每名玩家皆使用如下的混合策略：

使用(骑骑骑，步步步，弓弓弓，骑步骑，弓骑弓，步弓步，骑弓骑，步骑步，弓步弓)的概率分别为(6.9%,6.9%,6.9%,7.2%,7.2%,7.2%,19.2%,19.2%,19.2%)。

策略	骑,骑,骑	骑,骑,步	骑,骑,弓	骑,步,骑	骑,步,步	骑,步,弓	骑,弓,骑	骑,弓,步	骑,弓,弓
收益	0	-0.017	-0.018	0	-0.009	-0.078	0	-0.042	-0.023

在这种情况下使用单兵种和双兵种的阵容兼而有之，但是三兵种的阵容彻底被压制。

2.4.攻击规则2下的结果

通过与上述计算类似的流程可以得到无加成时最佳策略为，以任意的概率使用（骑步弓，步弓骑，弓骑步，骑弓步，弓步骑，步骑弓，骑弓弓，步骑骑，弓步步）中的一种或多种阵容。

而有加成时单兵种阵容则占据统治地位。

2.5.对玩家的影响

通过上述两种战斗规则的计算我们发现3兵种混合阵容为平均战斗力最低的阵容，实际上鼓励玩家追求同兵种的搭配。简单分析一下这样做的好处：

一定程度上增加各个队伍之间的差异性，突出克制关系，增强策略性。
增加小的收集目标。

必须注意的是，纳什平衡并不是一个构造性的理论，因此并不能用来预测玩家的实际阵容分布比例。

微信公众号

微博

头条号

百家号

网易号

知乎号

浅析率土之滨中的伤害公式和兵种加成对玩家阵容的影响

微信公众号

微博

头条号