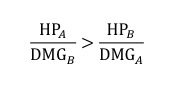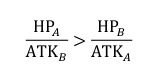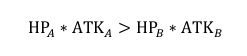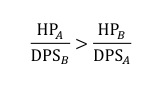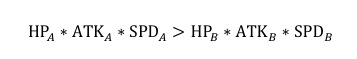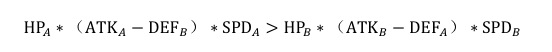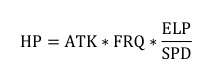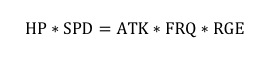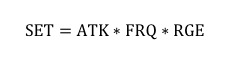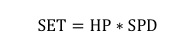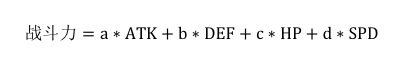作者:Einsphoton (任江枫)
关注以获得更多内容
版权所有,转载须注明出处以及作者
关键词:数值策划教程 数值策划入门 战斗力计算 数值规划 游戏数学模型 塔防数学模型
前言
有关于角色的战斗力,大家都不会陌生,几乎每一款游戏都有在计算相关角色的战斗力。 无论采用何种形式、方法,目的只有一个,就是想让玩家比较轻松直接的对比出角色的综合能力。
在这里,笔者将综合一些情况,与大家讨论一下战斗力的计算方法与有效性验证。
不过在这之前,按照惯例,还是先给大家讲一下个人的“扭曲”价值观与经验。
在日常工作中,我们总会发现有一些数值策划,他们的表格做的很漂亮,并且你点击任何 一个单元格,总会让你发现一长串让你无法继续阅读下去的公式,长到令人发指!这些数字环环 嵌套,相互关联,找了半天也很难找到计算的源头。这就是俗称【数值表格的关联性】,并且这 也广泛被业内定位为数值能力好坏的指标,或者招聘面试数值策划的标准。
笔者忍不住要吐槽,不过我想吐槽的不是【数值表格的关联性】而是这一【自动化】的设 计过程。
很幸运,我亲眼目睹了几个这样的表格,均出自大师之手。
所谓的数值规划,我个人理解的作用是——多人合作的时候,能够让其他策划看得懂你在 相关数值设计中的思路,并且也给自己一个总体纲要的规划。但是我看到的一份数值规划表格中, 所有数值全部都关联化,牵一动百,妄图将所有数值设计过程全部自动化。每一个层面,每一个 梯度,每一个兴奋点,每一个时间点,所有数值都存在着一个硬性的标杆公式强行控制每一个数 值。最后所有角色单位的数值也都与之前的“标尺”硬性关联,得出最终数值成品(虽然他还有 余力可以“微调”)。
笔者想说的是,游戏是一件艺术品,那里面承载了设计者的个性结晶。玩家的需求是在游 戏中获得挑战,获得惊喜,获得心意。不是一套自动化就可以得出的产物。自动化,就意味着里 面许多小细节设计者都忽视了。
最后那份数值产出,代入到产品中,大家看到了些许问题。他忽视了角色单位的差异性, 因为自动化导致了所有角色数值属性都是线性相关的;他忽视了关卡难度的兴奋感,因为所有关 卡数值全都是线性相关地上升,并且其中还会涉及到关卡的递进难度是否会超出预料的问题;他

只关注于武器、等级、缘分 BUFF 等综合能力占比,却忽视了这些能力组成在每个阶段变化不一, 所以在代入产品后,发现很多数值超出或低于期望。
笔者认为,一份好的数值规划,首先需要具有良好的易读性,因为这个不只是给你自己看 的,多数是给别人看的。其次它只起到
规划参考的作用,而不是标尺的作用,不要被自己的数值 规划限制住游戏数值的无限可能。我们制作数值规划的目的应该不会是让今后的数值都在规划数 值中乘以一个系数吧?最后代入产品中,发现处处硬坎,处处单一,然后以“数值不可能是一下 子就出来”的名义“微调”到底。
最后“微调”到亲爹亲妈(那份数值规划)都不认识的地步, 当初何苦花那么长的时间做一份那么华丽的数值规划,意义何在?
回归本文正题。
RPG 游戏中的战斗力计算模型
我们先考虑一种简单的模型。
游戏角色要想进行战斗计算,首先两个属性是必不可少的,HP、ATK。所以我们先模拟一下 只有 HP、ATK 参与计算的两人对战模型。定义:UnitName(HP,ATK)为一个战斗单位。先我 们有两个战斗单位,其中 UnitA(200,50),UnitB(400,20)。我们假定双方的攻击速度皆为每 单位时间(或者回合)行动一次。那么战斗过程可能为:
- 第一回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(180,50),UnitB(350,20)
- 第二回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(160,50),UnitB(300,20)
- 第三回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(140,50),UnitB(250,20)
- 第四回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(120,50),UnitB(200,20)
- 第五回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(100,50),UnitB(150,20)
- 第六回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(80,50),UnitB(100,20)
- 第七回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(60,50),UnitB(50,20)
- 第八回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(40,50),UnitB(0,20)
=====UnitB 战败======
我们稍微调整一下 UnitB 的数值,UnitB(400,25),再模拟一次战斗过程,看看会有什么变 化。(由于先手机制造成战斗结果不公平,所以在同一回合内,任一方的 HP 先为 0 判定为该方 战败,若双方 HP 同时为 0,则判定平均)
- 第一回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(175,50),UnitB(350,20)
- 第二回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(150,50),UnitB(300,20)
- 第三回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(125,50),UnitB(250,20)
- 第四回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(100,50),UnitB(200,20)
- 第五回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(75,50),UnitB(150,20)
- 第六回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(50,50),UnitB(100,20)
- 第七回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(25,50),UnitB(50,20)
- 第八回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(0,50),UnitB(0,20)
=====双方战平======
我们再来为 UnitB 调整一下数值,UnitB(500,20),再模拟一次战斗过程。
- 第一回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(180,50),UnitB(450,20)
- 第二回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(160,50),UnitB(400,20)
- 第三回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(140,50),UnitB(350,20)
- 第四回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(120,50),UnitB(300,20)
- 第五回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(100,50),UnitB(250,20)
- 第六回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(80,50),UnitB(200,20)
- 第七回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(60,50),UnitB(150,20)
- 第八回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(40,50),UnitB(100,20)
- 第九回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(20,50),UnitB(50,20)
- 第十回合 UnitA 攻击 UnitB,UnitB 攻击 UnitA【结果为】UnitA(0,50),UnitB(0,20)
=====双方战平=====
从以上三个结果中,读者们可能会发现一些规律,现在我们将对这个模型进行数学抽象。
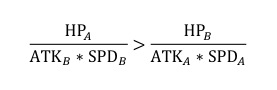
在只有 HP、ATK 两个属性参与战斗计算的过程中,我们判定一方战败的依据是其 HP 为 0。 在一场双角色 A、B 对砍的战斗模型中,判定角色 A 胜利的依据是,谁坚挺的时间长(HP 最后 变为 0 的一方)谁获得胜利:
即
得
由此我们得出,只有当一方角色单位的值 HP*ATK 大于另一方角色单位的值 HP*ATK 才能获得胜 利。
因此我们将角色单位的值 HP*ATK 定义为战斗力。 我们回头根据上面的 3 场战斗来验证一下结论是否一致?
一个战斗过程的简化运用
两个战斗单位的战斗过程,就是双方战斗力相减的过程。举例:
有两个单位 UnitA(200,50),UnitB(300,20),经过战斗力的计算,得 UnitA:10000,UnitB:6000。根据战斗力显示,UnitA 会获得明显的胜利。
这里有一个方法,可以直接简化战斗过程运算得出结果,我们将双方的战斗力相减,的UnitA的剩余战斗力为4000。按照之前的公式,将这个剩余战斗力除以UnitA的ATK属性,就会获得UnitA的HP属性。根据计算得,UnitA获胜,并且剩余HP为80。请读者自行验证。
基于基础战斗模型引入 SPD(速度)值
多数游戏对于速度值 SPD 的定义为,该角色单位时间的行动次数 times/time,或者定义为FQR(频率值)。(对于其他的速度值的定义请向此方向转换) 那么基于之前的结论,若角色 A 想要胜出,则:
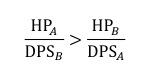
即
得
由此得出,只有一方角色单位的属性值 HP*ATK*SPD 大于另一方角色单位的属性值 HP*ATK*SPD 才能获得胜利。

同样的我们将角色单位的值 HP*ATK*SPD 定义为该角色的战斗力。 由于模型同理,笔者将不在这里赘述验证过程,请读者自己验证。
基于基础战斗模型引入 DEF(防御)值
在这种情况下,模型变得有些复杂,因为战斗结果不再那么纯粹,一方的战斗力是受对方影响的,为
相对战斗力。
这里我们一伤害公式 ATK-DEF 为例进行证明,其他公式所得出的结果虽不同,但是同理。 若 A 胜出,则:
即:
得
到这里,我们可以观察出,一方的战斗力是如何受对方影响的。
在这种情况下,我们称,该角色的战斗力是
相对的,而非
绝对的。
如何在相对中寻找绝对(适用环境局限,需待多方验证)
从以上的分析中,我们可以看出,在有 DEF 属性参与战斗计算的时候,一方的战斗力不是 一个定值,并且,三个单位的战斗力也不具有传递性。例如:
我们定义一个战斗单位,UnitName(HP,ATK,DEF,SPD)。
有如下 3 个战斗单位,UnitA(200,30,10,1),UnitB(450,20,15,0.5),UnitC(200,20,5,3)。
经过计算,我们发现三方的战斗力关系是,A>B,B>C,但却 C>A。
这是由于,UnitC 的攻击与 UnitB 的防御的差值过小,以至于 UnitC 的每一份攻防差的收益 过低,造成了 UnitC 出乎意料的输给了 UnitB。
这种现象不可避免。但是,通过多次试验以及分析函数图像得出,当攻击力远远大于防御 力的时候,这种现象发生的机会将会变少,并且有理由相信,在极限状态下,这种现象将不会存 在。

因此,我们可以人为的在规划数值的时候,将攻防的差距尽量拉大。从而减少这种现象的 发生。
不过,这种现象也是一种策略性的玩法,因为它符合石头剪刀布的封闭克制关系。
塔防游戏中的战斗力计算模型
笔者在之前的文章中已经较为系统的给出了塔防的数学模型,只是那篇文章写的较早,以 现在的眼光看来,比较杂乱无章,所以整理好思路,重新总结一遍。
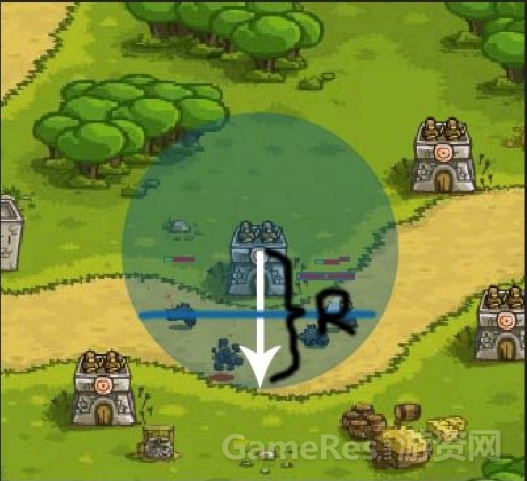
我们定义防御塔拥有三个属性,TowerName(ATK,FRQ,RGE),敌方单位 UnitName(HP, SPD)。已知,敌方单位总是穿过防御塔的攻击范围与路径的交集,在这里我们定义为 ELP(The Effective Length of Path)。
若,我方防御塔刚好能够杀死敌方一个单位,则用数学表达式抽象为:
由于,在多数情况下,ELP 的长度都与防御塔的范围半径相近,所以有
得

![]()
这样,我们得出了一个完美对称的等式,左边全都是敌方单位的属性,而右边全都是防御塔的属 性。因此我们定义一个值 SET 作为衡量双方的战斗力大小的值。对于防御塔来说,其战斗力为
对于地方单位来说,其战斗力为
当防御塔 ATK*FRQ*RGE 大于敌方单位 HP*SPD 时,则防御塔能够在无干扰的环境下轻松杀死敌 方一个单位;当防御塔 ATK*FRQ*RGE 等于敌方单位 HP*SPD 时,则防御塔能够在无干扰的环境 下刚好杀死一个单位;当防御塔 ATK*FRQ*RGE 小于敌方单位 HP*SPD 时,则防御塔很难杀死一 个敌方单位。
多个防御塔攻击一个敌方单位
在这种情况下,由于各个防御塔之间不互相干扰,所以所有防御塔可进行战斗力的加法运 算来衡量我方总战斗力是否能够杀死该敌方单位。
多个防御塔攻击多个敌方单位
在这种情况下,模型会变得稍微复杂,我们将不能简单的进行加法运算从而对比防御塔与 敌方单位战斗力的大小。
这是因为,防御塔的“抬手效应”与敌方单位的队伍间隔会极大影响战斗结果,试想一种 极端情况下,10 个敌方单位聚集在一小块范围下移动,当防御塔击杀第一个敌方单位的时候, 再也无力击杀下一个单位。
不过,为了考虑到设计游戏的实际操作性,我们通常会合理规划每个敌方单位的间隔距离, 从而使得方便计算。在这种理想状态下,该模型还是可以良好运行的。
横向对比现有的游戏
之前看到很多游戏都有计算过战斗单位的战斗力,但是几乎所有都采用同样的一种方法 -------加权多项式。
这种方法原理是,游戏设计者评估一个战斗单位的每一项属性,并且把每一项属性顶一个 权值,最后以加法运算得出战斗力。如:
但笔者认为这种计算方式利弊并存。坏处是,这种计算方式并不科学,不能较为可观的衡量该角 色的战斗能力。好处是,这种计算方式直观容易理解,并且对比笔者总结的模型有一个最大的好 处,就是数值小,并且数值增长幅度也小。

所以笔者建议,以上数学模型适用于战斗平衡的调整以及数值规划。不建议让用户观看理 解。
结束语
至此,想要总结的模型都已结束。
不知道大家有没有关心这样一件事情,从以上两个模型,我们都可以看出数学等式的一种 对称美,就好像,被人刻意安排一样。但我认为这并不是一种巧合,我有理由相信对于其他类型 的游戏来说,其战斗力的计算同样为因式的基本模型。
其实游戏中的一些数学模型非常简单,只是大家很少去关注,去抽象,去总结。非常希望 有识之士能够一起来总结一些规律,一起来构建起这座大厦。为业内贡献一份力量。
注:关于RPG角色数值模型,参考自网易游戏理论研究室的相关资料,但略有修改。